
分析 利用诱导公式化简已知条件求出函数的解析式.
(1)利用同角三角函数基本关系式化简求解即可.
(2)利用函数的解析式,化简后平方即可推出结果.
解答 解:设f(x)=2sin(180°-x)+cos(-x)-sin(450°-x)+cos(90°+x)
=2sinx+cosx-cosx-sinx
=sinx.
(1)设f(α)=$\frac{1}{3}$,α∈(0°,180°),可得sin$α=\frac{1}{3}$,cosα=±$\frac{2\sqrt{2}}{3}$
tanα=$\frac{sinα}{cosα}$=±$\frac{\sqrt{2}}{4}$;
(2)若f(α)=2sinα-cosα+$\frac{1}{2}$,
可得:sinα-cosα=-$\frac{1}{2}$,
两边平方可得:1-2sinαcosα=$\frac{1}{4}$,
sinα•cosα=$\frac{3}{8}$.
点评 本题考查诱导公式以及同角三角函数基本关系式的应用,考查计算能力.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
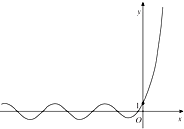 已知如下六个函数:y=x,y=x2,y=lnx,y=2x,y=sinx,y=cosx,从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=2x+sinx.
已知如下六个函数:y=x,y=x2,y=lnx,y=2x,y=sinx,y=cosx,从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=2x+sinx.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
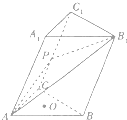 如图所示,在三棱柱ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.
如图所示,在三棱柱ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x=2时,x2-3x+2=0”的否命题 | |
| B. | “若α=β,则sinα=sinβ”的逆命题 | |
| C. | 平面α⊥平面α,平面γ⊥平面β,则平面α∥平面γ | |
| D. | “相似三角形的对应角相等”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com