
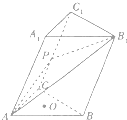
 如图所示,在三棱柱ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.
如图所示,在三棱柱ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.分析 (1)点A1在底面△ABC的射影为O,连接A1O,取BC的中点E,连接AE,利用线面垂直的性质定理可得A1O⊥BC.利用等边三角形的性质及其线面垂直的判定定理可得:BC⊥平面A1OA,可得BC⊥A1A,而AA1∥BB1,即可证明结论.
(2)由(1)知A1O,AO,BC两两垂直,建立如图所示的空间直角坐标系,由于A1O⊥平面ABC,可得∠A1AO为A1A底面△ABC所成的角.求出平面PAB1的一个法向量,利用向量夹角公式即可得出.
解答 (1)证明:点A1在底面△ABC的射影为O,连接A1O,取BC的中点E,连接AE,
∵A1O⊥平面ABC,BC?平面ABC,∴A1O⊥BC.
又∵AE⊥BC,AE∩A1O=O,∴BC⊥平面A1OA,
∵AA1?平面A1OA,∴BC⊥A1A,
∵AA1∥BB1,∴BC⊥BB1.
(2)解:由(1)知A1O,AO,BC两两垂直,建立如图所示的空间直角坐标系,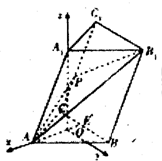
∵A1O⊥平面ABC,∴∠A1AO为A1A底面△ABC所成的角.
∵AB=6,∴$AO=\frac{{\sqrt{3}}}{3}×6=2\sqrt{3}$,$OE=\sqrt{3}$,$∠{A_1}AO={60^0}$,A1O=6,
∴$A(2\sqrt{3},0,0)$,$B(-\sqrt{3},3,0)$,$C(-\sqrt{3},-3,0)$,A1(0,0,6),
$\overrightarrow{A{A_1}}=\overrightarrow{B{B_1}}=\overrightarrow{C{C_1}}=(-2\sqrt{3},0,6)$,$\overrightarrow{AC}=(-3\sqrt{3},-3,0)$,$\overrightarrow{AB}=(-3\sqrt{3},3,0)$,$\overrightarrow{AP}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{C{C_1}}=(-4\sqrt{3},-3,3)$,$\overrightarrow{A{B_1}}=\overrightarrow{AB}+\overrightarrow{B{B_1}}=(-5\sqrt{3},3,6)$,
设平面PAB1的一个法向量$\overrightarrow n=(x,y,z)$,由$\overrightarrow{AP}•\overrightarrow n=\overrightarrow{A{B_1}}•\overrightarrow n=0$,
得$\left\{{\begin{array}{l}{-4\sqrt{3}x-3y+3z=0}\\{-5\sqrt{3}x+3y+6z=0}\end{array}}\right.$,得$\overrightarrow n=(\sqrt{3},-1,3)$.
$|cos<\overrightarrow{n},\overrightarrow{B{B}_{1}}>|$=$\frac{|\overrightarrow{n}•\overrightarrow{B{B}_{1}}|}{|\overrightarrow{n}||\overrightarrow{B{B}_{1}}|}$=$\frac{12}{\sqrt{13}×\sqrt{48}}$=$\frac{{\sqrt{39}}}{13}$.
∴直线BB1与平面AB1P所成角的正弦值$\frac{{\sqrt{39}}}{13}$.
点评 本题考查了空间位置关系、线面面面垂直与平行的判定及其性质定理、空间角、向量夹角公式、法向量的应用、等边三角形的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 奇函数或偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},\frac{3}{2}})$ | B. | $[{1,\frac{5}{4}})$ | C. | $({1,\frac{3}{2}})$ | D. | $[{1,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{9}=1$ | C. | $\frac{y^2}{18}-\frac{x^2}{18}=1$ | D. | $\frac{x^2}{18}-\frac{y^2}{18}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com