
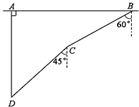
 如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离.
如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离. 分析 过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=$\frac{1}{2}$BC=$\frac{1}{2}$×1000=500米;解Rt△CDF,求出CF=$\frac{\sqrt{2}}{2}$CD=500$\sqrt{2}$米,则DA=BE+CF=(500+500$\sqrt{2}$)米.
解答 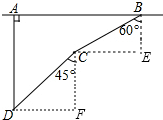 解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}×$1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,
∴CF=$\frac{\sqrt{2}}{2}$CD=500$\sqrt{2}$米,
∴DA=BE+CF=(500+500$\sqrt{2}$)米,
故拦截点D处到公路的距离是(500+500$\sqrt{2}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,正确理解方向角的定义,进而作出辅助线构造直角三角形是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | “x=2时,x2-3x+2=0”的否命题 | |
| B. | “若α=β,则sinα=sinβ”的逆命题 | |
| C. | 平面α⊥平面α,平面γ⊥平面β,则平面α∥平面γ | |
| D. | “相似三角形的对应角相等”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2f(-2)<-ef(-e)<3f(3) | B. | -ef(-e)<-2f(-2)<3f(3) | C. | 3f(3)<-ef(-e)<-2f(-2) | D. | -2f(-2)<3f(3)<-ef(-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
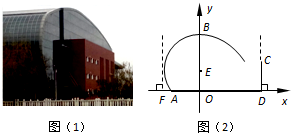 某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.
某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com