
| A. | -2f(-2)<-ef(-e)<3f(3) | B. | -ef(-e)<-2f(-2)<3f(3) | C. | 3f(3)<-ef(-e)<-2f(-2) | D. | -2f(-2)<3f(3)<-ef(-e) |
分析 由已知可构造函数g(x)=xf(x),求其导函数,可得g(x)=xf(x)在(0,+∞)上为增函数,则在(-∞,0)上为减函数.然后由g(-3)>g(-e)>g(-2)得答案.
解答 解:∵函数f(x)是定义在R上的奇函数,f(-x)=-f(x)
令g(x)=xf(x),
∴g(-x)=g(x)是定义在R上的偶函数,
又当当x>0时恒有f(x)+xf′(x)>0,即g′(x)>0,
∴g(x)=xf(x)在(0,+∞)上为增函数,则在(-∞,0)上为减函数.
∴g(-3)>g(-e)>g(-2),即g(3)>g(-e)>g(-2),
∴3f(3)>-ef(-e)>-2f(-2),即-2f(-2)<-ef(-e)<3f(3).
故选:A.
点评 本题考查利用导数研究函数的单调性,考查了函数构造法,是中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
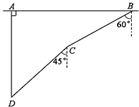 如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离.
如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| B. | 命题“若x=0,则x2-x=0”逆否命题为真命题 | |
| C. | 若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n | |
| D. | 若“p∧q”为假命题,则“p∨q”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $2-\frac{{\sqrt{2}}}{2}$ | D. | $2+\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com