
| A. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| B. | 命题“若x=0,则x2-x=0”逆否命题为真命题 | |
| C. | 若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n | |
| D. | 若“p∧q”为假命题,则“p∨q”为真命题 |
分析 直接写出命题的否命题判断A;直接写出命题的逆否命题判断B;写出特称命题的否定判断C;由复合命题的真假判断判断D.
解答 解:命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”,故A正确;
命题“若x=0,则x2-x=0”为真命题,则逆否命题为真命题,故B正确;
若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n,故C正确;
若“p∧q”为假命题,则p、q中至少一个为假命题,则“p∨q”不一定为真命题,故D错误.
∴错误的命题是D.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的否定与逆否命题,考查复合命题的真假判断,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x=2时,x2-3x+2=0”的否命题 | |
| B. | “若α=β,则sinα=sinβ”的逆命题 | |
| C. | 平面α⊥平面α,平面γ⊥平面β,则平面α∥平面γ | |
| D. | “相似三角形的对应角相等”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2f(-2)<-ef(-e)<3f(3) | B. | -ef(-e)<-2f(-2)<3f(3) | C. | 3f(3)<-ef(-e)<-2f(-2) | D. | -2f(-2)<3f(3)<-ef(-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
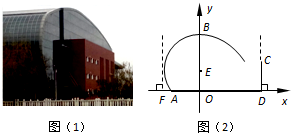 某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.
某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com