
分析 将行列式按第二行展开,求得不等式=$\frac{x}{x-1}$+2≥0,注意对数函数的定义域.
解答 解:$|{\begin{array}{l}1&0&0\\{lgx}&{\frac{1}{x-1}}&{-2}\\ 1&1&x\end{array}}|≥0$等价于lgx$|\begin{array}{l}{0}&{0}\\{1}&{x}\end{array}|$+$\frac{1}{x-1}$$|\begin{array}{l}{1}&{0}\\{1}&{x}\end{array}|$+2$|\begin{array}{l}{1}&{0}\\{1}&{1}\end{array}|$=$\frac{x}{x-1}$+2≥0,
即$\left\{\begin{array}{l}{x>0}\\{\frac{x}{x-1}+2≥0}\end{array}\right.$,
解得0<x≤$\frac{2}{3}$或x>1,
故不等式的解集为$(0,\frac{2}{3}]∪(1,+∞)$.
故答案为:$(0,\frac{2}{3}]∪(1,+∞)$.
点评 本题考查行列式的展开,考查不等式的解集,考查计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| B. | 命题“若x=0,则x2-x=0”逆否命题为真命题 | |
| C. | 若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n | |
| D. | 若“p∧q”为假命题,则“p∨q”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
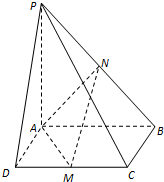 如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,
如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com