练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知（3x-1）7=a0x7+a1x6+…+a6x+a7，则a0+a2+a4+a6=8256．

    分析 分别令x=1，-1即可得出．

    解答 解：（3x-1）7=a0x7+a1x6+…+a6x+a7，
    令x=1，则27=（3-1）7=a0+a1+…+a6+a7，
    令x=-1可得：-47=-a0+a1-…-a6+a7，
    ∴2（a0+a2+a4+a6）=27+47=8256，
    故答案为：8256．

    点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

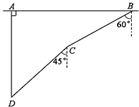    14．如图，在一次军事演习中，蓝方在一条东西走向公路上的A处朝正南方撤退，红方在公路B处沿南偏西60°方向实施拦截，红方行驶1000米到C处，发现前方无法通行，决定调整方向再朝南偏西45°方向前进了相同的距离，刚好在D处拦截到蓝方，求拦截点D到公路的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）是定义在[a-1，2a]上的偶函数，且当x＞0时，f（x）单调递增，则关于x的不等式f（x-1）＞f（a）的解集为[$\frac{1}{3}$，$\frac{2}{3}$）∪（$\frac{4}{3}$，$\frac{5}{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在平面直角坐标系中，已知A（-1，2），B（2，1），C（1，0）．
    （Ⅰ）判定三角形ABC形状；
    （Ⅱ）求过点A且在x轴和在y轴上截距互为倒数的直线方程；
    （Ⅲ）已知l是过点A的直线，点C到直线l的距离为2，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．要证：a2+b2-1-a2b2≥0，只要证明（　　）
    A．2ab-1-a2b2≥0B．（a2-1）（b2-1）≥0
    C．$\frac{（a+b）2}{2}$-1-a2b2≥0D．a2+b2-1-$\frac{{a}^{4}+{b}^{4}}{2}$≤0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．在极坐标系下，点$A（2，\frac{3π}{4}）$到直线l：ρcos（θ-$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$的距离为（　　）
    A．$\sqrt{2}$B．$\frac{{\sqrt{2}}}{2}$C．$2-\frac{{\sqrt{2}}}{2}$D．$2+\frac{{\sqrt{2}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在△ABC中，角A，B，C所对的边为a，b，c，设S为△ABC的面积，满足S=$\frac{{\sqrt{3}}}{4}（{a^2}+{c^2}-{b^2}）$
    （1）求角B的大小
    （2）求sinA+sinC的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．现有2位男生和3位女生共5位同学站成一排．（用数字作答）
    （1）若2位男生相邻且3位女生相邻，则共有多少种不同的排法？
    （2）若男女相间，则共有多少种不同的排法？
    （3）若男生甲不站两端，女生乙不站最中间，则共有多少种不同的排法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．如图是一几何体的直观图、正视图和俯视图．下列选项图中，按照画三视图的要求画出的该几何体的侧视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案