
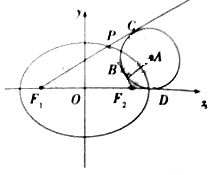
 如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )
如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 4$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
分析 根据切线的性质可得|PC|=|PB|,|F2B|=|F2D|,|F1C|=|F1D|,根据椭圆的定义可知:|PF1|+|PF2|=2a,进行等量代换可得|F1C|+|F1D|=2a+2c,根据椭圆的离心率为$\sqrt{3}$-1,a=2,即可求出c的值,进而求出|F1C|的值;设∠PF2F1=θ,则45°<θ<90°,在Rt△PF1F2中,结合|PF1|+|PF2|=2a可得2ccosθ+2csinθ=2a,进而求出θ=60°,得到|PF1|的值,即可求得圆A的半径.
解答 解:∵圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,
∴|PC|=|PB|,|F2B|=|F2D|,|F1C|=|F1D|.
由椭圆的定义可知:|PF1|+|PF2|=2a,
∴|PF1|+|PC|+|F2D|=2a,即|F1C|+|F1D|=2a+2c,
∴|F1C|=|F1D|=a+c.
椭圆的离心率为$\sqrt{3}$-1,a=2,
∴c=2($\sqrt{3}$-1),
∴|F1C|=|F1D|=a+c=2$\sqrt{3}$
又∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
则∠F1PF2=90°.设∠PF2F1=θ.
∵P是椭圆上第一象限内的一点,45°<θ<90°,
∴2ccosθ+2csinθ=2a,即cosθ+sinθ=$\frac{a}{c}$=$\frac{\sqrt{3}+1}{2}$,
∴1+sin2θ=($\frac{\sqrt{3}+1}{2}$)2=1+$\frac{\sqrt{3}}{2}$,
∴sin2θ=$\frac{\sqrt{3}}{2}$,解得θ=60°,
∴|PF1|=2csinθ=$\sqrt{3}$c,
∴圆A的半径为|F1C|-|PF1|=2$\sqrt{3}$-$\sqrt{3}$×2($\sqrt{3}$-1)=4$\sqrt{3}$-6.
故选B.
点评 本题考查椭圆的定义及性质的综合应用,圆的切线性质,三角形函数的应用,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$] | B. | (-∞,e] | C. | $({\frac{1}{e},+∞})$ | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=$\root{3}{x}$,g(x)=$\frac{{x}^{2}}{x}$ | C. | f(x)=lnex,g(x)=elnx | D. | f(x)=$\frac{1}{|x|}$,g(x)=$\frac{1}{\sqrt{{x}^{2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com