
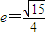 ,左顶点A(-4,0),圆O':(x-2)2+y2=r2是椭圆G的内接△ABC的内切圆.
,左顶点A(-4,0),圆O':(x-2)2+y2=r2是椭圆G的内接△ABC的内切圆.
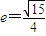 ,左顶点A(-4,0),可求椭圆的标准方程;
,左顶点A(-4,0),可求椭圆的标准方程;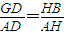 即
即 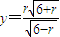 ,再由点B(2+r,y)在椭圆上,建立关于r的方程求解.
,再由点B(2+r,y)在椭圆上,建立关于r的方程求解.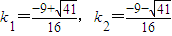 ,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.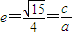 ,a=4得
,a=4得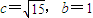 ,椭圆G方程为
,椭圆G方程为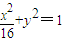 -------(5分)
-------(5分)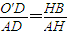 得
得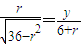 ,即
,即 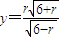 (1)---------(7分)
(1)---------(7分)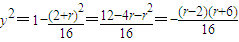 (2)-----(9分)
(2)-----(9分)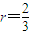 或
或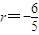 (舍去)-------(11分)
(舍去)-------(11分)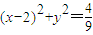 相切的直线方程为:y-1=kx(3)
相切的直线方程为:y-1=kx(3)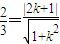 ,即32k2+36k+5=0(4)
,即32k2+36k+5=0(4)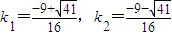
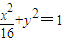 得(16k2+1)x2+32kx=0,则异于零的解为
得(16k2+1)x2+32kx=0,则异于零的解为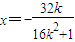 -------(13分)
-------(13分)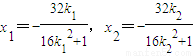
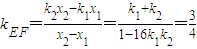
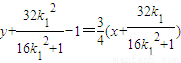 即
即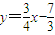
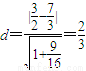 故结论成立.------------(15分)
故结论成立.------------(15分)

科目:高中数学 来源: 题型:
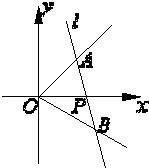 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直角坐标系中,直线y=6-x与y=
如图,在直角坐标系中,直线y=6-x与y=| 4 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
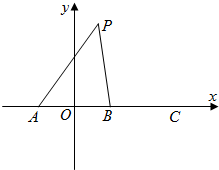 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.| x |
| 3 |
| y | ||
2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
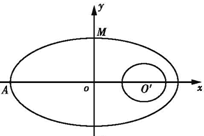 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
| ||
| 4 |
| 4 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com