练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，椭圆的离心率为，以椭圆的上顶点为圆心作圆，

    ，圆与椭圆在第一象限交于点,在第二象限交于点.

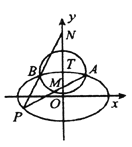
    （1）求椭圆的方程；

    （2）求的最小值，并求出此时圆的方程；

    （3）设点是椭圆上异于的一点，且直线分别与轴交于点为坐标原点，求证:

    为定值.

    【答案】（1）；（2）；（3）详见解析.

    【解析】试题分析：（1）依据题设条件求出参数即可；（2）依据题设条件及向量的数量积公式建立目标函数，再借助该函数取得最小值时求出圆的方程；（3）借助直线与椭圆的位置关系进行分析推证：

    试题解析：

    (1) 由题意知， ,得.

    故椭圆的方程为.

    (2) 点与点关于轴对称，设，由点椭圆上，则,得

    .由题意知， ,当时， 取得最小值.此时， ，故.又点在圆上，代入圆的方程，得.

    故圆的方程为.

    （3）设，则的方程为.令，得.同理可得， . 故. ①

    都在椭圆上， ,代入①得， .即得为定值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

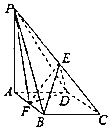
    【题目】如图：在四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=3，PA⊥底面ABCD，E是PC中点，F是AB中点．

    （Ⅰ）求证：BE∥平面PDF；

    （Ⅱ）求直线PD与平面PFB所成角的正切值；

    （Ⅲ）求三棱锥P﹣DEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知抛物线的顶点在坐标原点，对称轴为轴，焦点为,抛物线上一点的横坐标为，且.

    （Ⅰ）求此抛物线的方程；

    （Ⅱ）过点做直线交抛物线于两点,求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】轮船从某港口将一些物品送到正航行的轮船上，在轮船出发时，轮船位于港口北偏西且与相距20海里的处，并正以30海里的航速沿正东方向匀速行驶，假设轮船沿直线方向以海里/小时的航速匀速行驶，经过小时与轮船相遇.

    （1）若使相遇时轮船航距最短，则轮船的航行速度大小应为多少？

    （2）假设轮船的最高航速只能达到30海里/小时，则轮船以多大速度及什么航行方向才能在最短时间与轮船相遇，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大理石工厂初期花费98万元购买磨大理石刀具，第一年需要各种费用12万元，从第二年起，每年所需费用比上一年增加4万元，该大理石加工厂每年总收入50万元.

    （1）到第几年末总利润最大，最大值是多少？

    （2）到第几年末年平均利润最大，最大值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆心为 的圆过点和，且圆心在直线： 上.

    （1）求圆心为的圆的标准方程；

    （2）过点 作圆的切线，求切线方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在[﹣1，1]上的奇函数f（x），已知当x∈[﹣1，0]时的解析式f（x）= ﹣ （a∈R）．
    （1）写出f（x）在[0，1]上的解析式；
    （2）求f（x）在[0，1]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆与圆

    （1）若直线与圆相交于两个不同点，求的最小值；

    （2）直线上是否存在点，满足经过点有无数对互相垂直的直线和，它们分别与圆和圆相交，并且直线被圆所截得的弦长等于直线被圆所截得的弦长？若存在，求出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂拟生产甲、乙两种适销产品，每件销售收入分别为3万元、2万元，甲、乙产品都需要在两种设备上加工，在每台上加工1件甲所需工时分别是1、2，加工1件乙所需工时分别为2、1， 两种设备每月有效使用台时数分别为400和500，如何安排生产可使收入最大？

    查看答案和解析>>

    同步练习册答案