
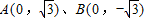 的距离之和为4.
的距离之和为4. 的距离之和为4.
的距离之和为4.
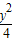 =1;
=1; y′,∴x′=x,y′=2y
y′,∴x′=x,y′=2y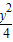 =1上,
=1上,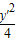 =1,即x2+y2=1
=1,即x2+y2=1

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
已知P是椭圆 =1(a>b>0)上一点,
=1(a>b>0)上一点, 是椭圆的焦点,
是椭圆的焦点, ,且点P到两准线的距离分别为
,且点P到两准线的距离分别为

(Ⅰ)求椭圆的准线方程;
(Ⅱ)求椭圆的方程;
(Ⅲ)又若已知定点B( )、C(
)、C( ),Q(
),Q( )是椭圆上一动点(
)是椭圆上一动点( >0),QH⊥x轴,垂足为H,∠BQH=α,∠HQC=β.
>0),QH⊥x轴,垂足为H,∠BQH=α,∠HQC=β.
求tan(α+β)的最小值,并求此时Q点的坐标.
查看答案和解析>>
科目:高中数学 来源:2010年湖南师大附中高二上学期模块结业考试数学文卷 题型:解答题
(本小题满分12分)
若一动点F到两定点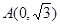 、
、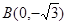 的距离之和为4.
的距离之和为4.
(Ⅰ)求动点F的轨迹方程;
(Ⅱ)设动点F的轨迹为曲线C,在曲线C任取一点P,过点P作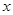 轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?
轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com