【答案】
分析:①函数是一个分式函数,分母不为零即可,考查分母即可得出定义域;
②由于函数是一个根式函数,可令
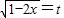
进行换元,将根式函数变为二次函数,利用二次函数性质求值域;
③由函数的形式,可等式两边同乘以分母,将函数值y看作常数,由此可转化出一元二次方程,此方程有根,其判别式大于等于0,由此即可得到关于y的不等式,解不等式即可得到函数的值域.
解答:解:①.因为|x+1|+|x-1|的函数值一定大于0,且x-1无论取什么数三次方根一定有意义,故其值域为R;
②.令
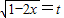
,t≥0,
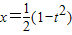
,原式等于
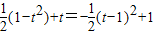
,故y≤1.
③.把原式化为以x为未知数的方程(y-2)x
2-(y-2)x+y-3=0,
当y≠2时,△=(y-2)
2-4(y-2)(y-3)≥0,得
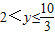
;
当y=2时,方程无解;所以函数的值域为
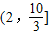
.
点评:本题考查函数的定义域与值域,解答的关键是掌握住定义域时常用的一些限制条件如分母不为零、偶次根号下非负等,第二小题求值域用到了换元法,将求函数值域的问题转化为常见函数的值域,降低了题目难度,第三题用到了判别式法求值域,这是二次型分式常用的求值域的技巧,要注意总结其使用的规则.

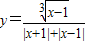 的定义域;
的定义域;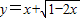 的值域;
的值域;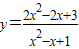 的值域.
的值域.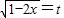 进行换元,将根式函数变为二次函数,利用二次函数性质求值域;
进行换元,将根式函数变为二次函数,利用二次函数性质求值域;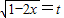 ,t≥0,
,t≥0,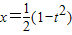 ,原式等于
,原式等于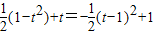 ,故y≤1.
,故y≤1.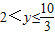 ;
;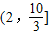 .
.
