
 如图所示的多面体是由底面为ABCD的长方体被截面AEC′F所截而得到的,其中AB=BC=CC′=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC′F所截而得到的,其中AB=BC=CC′=3,BE=1.分析 (Ⅰ)根据面面平行的性质定理得出AE∥C′F,AF∥C′E,故四边形AEC′F是平行四边形;
(Ⅱ)将几何体补成正方体,则几何体的体积为正方体体积的一半.
解答 证明:(Ⅰ)∵平面ABE∥平面DCC′F,平面AEC′F∩平面ABE=AE,平面AEC′F∩平面DCC′F=C′F,
∴AE∥C′F,
同理可得AF∥C′E,
∴四边形AEC′F是平行四边形.
(Ⅱ)将几何体补成棱长为3的正方体,
∴几何体ABCDEC'F的体积V=$\frac{1}{2}$V正方体=$\frac{1}{2}$×33=$\frac{27}{2}$.
点评 本题考查了面面平行的性质,几何体的体积计算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
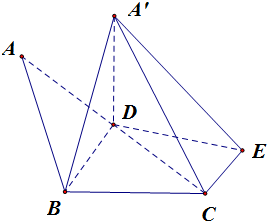 在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$.
在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?
小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 50 | 60 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 80 | 110 |
| K2≥k | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com