
如图, 为圆
为圆 的直径,
的直径, 为垂直于
为垂直于 的一条弦,垂足为
的一条弦,垂足为 ,弦
,弦 与
与 交于点
交于点 .
.
(Ⅰ)证明: 四点共圆;
四点共圆;
(Ⅱ)证明: .
.
(Ⅰ)证明过程详见解析;(Ⅱ)证明过程详见解析.
解析试题分析:本题考查四点共圆的判定和圆割线的性质.考查学生的分析问题解决问题的能力.第一问是证明四点共圆,证明四点共圆的基本方法:1.从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆.2.若能证明其顶角相等(同弧所对的圆周角相等),从而即可肯定这四点共圆.3.把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆.4.把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆(相交弦定理的逆定理);或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.(割线定理的逆定理)5.证被证共圆的点到某一定点的距离都相等,从而确定它们共圆.既连成的四边形三边中垂线有交点,即可肯定这四点共圆.上述五种基本方法中的每一种的根据,就是产生四点共圆的一种原因,因此当要求证四点共圆的问题时,首先就要根据命题的条件,并结合图形的特点,在这五种基本方法中选择一种证法,给予证明.第二问是等式的证明,这一问中遇到的圆割线的性质(从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等)、相似三角形、勾股定理三式联立,证明等式成立.
试题解析:(Ⅰ)连结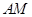 ,则
,则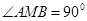 .因为
.因为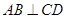 ,所以
,所以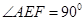 .
.
所以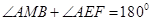 ,即
,即 四点共圆. 5分
四点共圆. 5分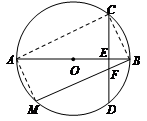
(Ⅱ)连结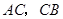 .由
.由 四点共圆,所以
四点共圆,所以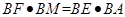 .在
.在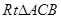 中,
中,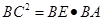 ,
,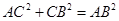 ,所以
,所以 . 10分
. 10分
考点:1.四点共圆的判断;2.圆割线的性质.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形;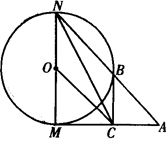
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AB、CD是⊙O的两条平行切线,B、D为切点,AC为⊙O的切线,切点为E.过A作AF⊥CD,F为垂足.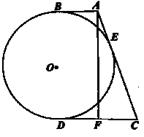
(1)求证:四边形ABDF是矩形;
(2)若AB=4,CD=9,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com