
已知双曲线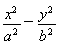 =1(a>0,b>0)的一个焦点与抛物线y2=4
=1(a>0,b>0)的一个焦点与抛物线y2=4 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.x2- =1 B.x2-y2=15 C.
=1 B.x2-y2=15 C. -y2=1 D.
-y2=1 D.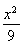 -
-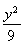 =1
=1
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
一次射击训练,某小组的成绩只有7环、8环、9环三种情况,且该小组的平均成绩为8.15环,设该小组成绩为7环的有x人,成绩为8环、9环的人数情况见下表:
环数(环) | 8 | 9 |
人数(人) | 7 | 8 |
那么x=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:填空题
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
过双曲线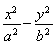 =1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=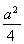 的切线,交双曲线右支于点P,切点为E,若
的切线,交双曲线右支于点P,切点为E,若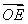 =
=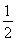 (
(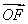 +
+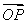 ),则双曲线的离心率为( )
),则双曲线的离心率为( )
A. 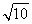 B.
B. 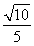 C.
C. 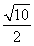 D.
D.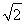
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
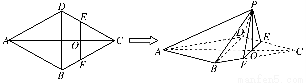
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:填空题
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于点O,剪去△AOB,将剩余部分沿OC,OD折叠,使OA,OB重合,则以A,B,C,D,O为顶点的四面体的体积为________.
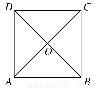
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
已知函数f(x)= .
.
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意m∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com