
(Ⅱ)设x、y均为正实数,证明不等式:(x+y)ln![]() ≤xlnx+ylny.
≤xlnx+ylny.
解:(Ⅰ)解法一:
因为ax>0,a>0,所以![]() 中
中
当且仅当ax=a,即x=1时,上式等号成立,
所以f(x)≥0对任意的x∈![]() 恒成立,
恒成立,
所以,当且仅当x=1时,f(x)取最小值
解法二:
![]() (x)=
(x)=![]()
当x>1时,x>![]() 成立
成立
若a>1,则lna>0,ax-![]() >0;
>0;
若0<a<1,则lna<0,ax-![]() <0.所以
<0.所以![]() (x)>0
(x)>0
即函数f(x)在(1,+∞)上单调递增
又f(1)=0, 所以[f(x)]min=f(1)=0.
(Ⅱ)证明:
①当x=y时,(x+y)ln![]() =xlnx+ylny
=xlnx+ylny
②当x≠y时,不失一般性,设x>y>0并取y=m,则x∈(m,+∞).
设g(x)=xlnx+ylny-(x+y)ln![]()
即g(x)=xlnx-(x+m)ln![]() +mlnm,x∈(m,+∞)
+mlnm,x∈(m,+∞)
![]() (x)=lnx+1-(ln
(x)=lnx+1-(ln![]() +
+![]() ·
·![]() )
)
=lnx-ln![]() =ln
=ln![]()
因为2x>x+m>0 所以![]() >1
>1
所以![]() (x)=ln
(x)=ln![]() >0
>0
所以g(x)在(m,+∞)上单调递增
又g(m)=0
所以g(x)>0,即xlnx-(x+m)ln![]() +mlnm>0
+mlnm>0
所以(x+m)ln![]() <xlnx+mlnm
<xlnx+mlnm
即(x+y)ln![]() <xlnx+ylny.
<xlnx+ylny.
综合①,②,有不等式
(x+y)ln![]() ≤xlnx+ylny成立
≤xlnx+ylny成立


科目:高中数学 来源: 题型:
|
| lim |
| x→a- |
查看答案和解析>>
科目:高中数学 来源:温州一模 题型:填空题
|
| lim |
| x→a- |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:江苏省高考数学一轮复习单元试卷03:指数函数与对数函数(解析版) 题型:解答题
 (x≥1)
(x≥1)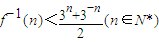 ,求a的取值范围.
,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com