练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等差数列{an}中，a1＞0，且3a8=5a13，则满足Sn＞0的n的最大值为（ ）
    A．40
    B．39
    C．21
    D．20
    【答案】分析：由题意可得：等差数列的公差d＜0，结合题意可得a1=-19.5d，可得Sn=0.5dn2-20dn，进而结合二次不等式的性质求出答案．
    解答：解：由题意可得：等差数列的Sn为二次函数，依题意是开口向下的抛物线故有最大值，
    所以等差数列的公差d＜0．
    因为a13=a8+5d，
    所以a1=-19.5d
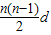
    由Sn=n×a1+可得Sn=0.5dn2-20dn，
    所以令Sn=0.5dn2-20dn＞0可得：0＜n＜40．
    故选B．
    点评：本题是一个最大值的问题，主要是利用等差数列的性质与等差数列的前n项和的公式以及结合二次函数的性质来解题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案