
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f′(x))′,若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0, )上不是凸函数的是________.
)上不是凸函数的是________.
①f(x)=sim x+cos x ②f(x)=ln x-2x
③f(x)=x3+2x-1 ④f(x)=x·ex
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:选择题
掷一枚均匀的硬币两次,事件M:一次正面朝上,一次反面朝上,事件N:至少一次正面朝上,则下列结果正确的是( )
A.P(M)= ,P(N)=
,P(N)= B.P(M)=
B.P(M)=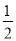 ,P(N)=
,P(N)=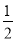
C.P(M)=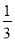 ,P(N)=
,P(N)=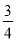 D.P(M)=
D.P(M)=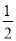 ,P(N)=
,P(N)=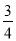
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:选择题
三张卡片的正反面分别写有1和2,3和4,5和6,若将三张卡片并列,可得到不同的三位数(6不能作9用)的个数为( )
A.8 B.6 C.14 D.48
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:选择题
已知集合A={x∈R| ≤0},B={x∈R|(x-2a)(x-a2-1)<0}.若A∩B=∅,则实数a的取值范围是( )
≤0},B={x∈R|(x-2a)(x-a2-1)<0}.若A∩B=∅,则实数a的取值范围是( )
A.(2,+∞) B.[2,+∞)
C.{1}∪[2,+∞) D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
若存在实常数k和b,使得函数f(x)和g(x)对其定义域上的任意实数x分别满足:f(x)≥kx+b和g(x)≤kx+b,则称直线l:y=kx+b为f(x)和g(x)的“隔离直线”.已知h(x)=x2,φ(x)=2eln x(其中e为自然对数的底数),根据你的数学知识,推断h(x)与φ(x)间的隔离直线方程为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
已知数列{an}:a1,a2,a3,…,an,如果数列{bn}:b1,b2,b3,…,bn满足b1=an,bk=ak-1+ak-bk-1,其中k=2,3,…,n,则称{bn}为{an}的“衍生数列”.若数列{an}:a1,a2,a3,a4的“衍生数列”是5,-2,7,2,则{an}为________;若n为偶数,且{an}的“衍生数列”是{bn},则{bn}的“衍生数列”是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
如图,直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,这个函数的图像大致是________(填序号).
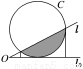
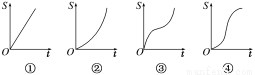
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:选择题
一个正方体截去两个角后所得几何体的正视图、侧视图如图所示,则其俯视图为( )

查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-2同角三角函数基本关系式与诱导公式(解析版) 题型:选择题
已知α∈(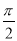 ,π),tanα=-
,π),tanα=-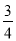 ,则sin(α+π)=( )
,则sin(α+π)=( )
A.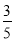 B.-
B.-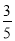 C.
C.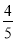 D.-
D.-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com