已知圆.圆.动圆与圆外切并与圆内切.圆心的轨迹为曲线 .(1)求的方程,(2)若直线与曲线交于两点.问是否在轴上存在一点.使得当变动时总有?若存在.请说明理由. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

已知圆，圆，动圆与圆外切并与圆内切，圆心的轨迹为曲线 .

（1）求的方程；

（2）若直线与曲线交于两点，问是否在轴上存在一点，使得当变动时总有？若存在，请说明理由.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2015-2016学年河南南阳一中高二下第二次月考理科数学卷（解析版） 题型：解答题

将一个半径适当的小球放入如图所示的容器最上方的入口处, 小球将自由下落, 小球在下落过程中, 将次遇到黑色障碍物, 最后落入内袋或外袋中, 已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.

（1）求小球落入袋中的概率；

（2）在容器入口处依次放入个小球, 记为落入袋中小球的个数，试求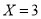的概率和的数学期望.

查看答案和解析>>

科目：高中数学 来源：2015-2016学年山东省高一6月月考数学试卷（解析版） 题型：选择题

化简得（）

A． B． C． D．

查看答案和解析>>

科目：高中数学 来源：2016届安徽省高三下学期冲刺模拟文科数学A卷（解析版） 题型：选择题

已知函数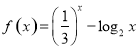，实数满足若实数为方程的一个解，那么下列不等式中，不可能成立的是（）

A． B． C． D．

查看答案和解析>>

科目：高中数学 来源：2016届安徽省高三下学期冲刺模拟文科数学A卷（解析版） 题型：选择题

“”是“”的（）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

查看答案和解析>>

科目：高中数学 来源：2016届安徽省高三下学期冲刺模拟理科数学A卷（解析版） 题型：填空题

若的展开式所有的系数之和为81，则直线与曲线所围成的封闭区域面积为__________.

查看答案和解析>>

科目：高中数学 来源：2016届安徽省高三下学期冲刺模拟理科数学A卷（解析版） 题型：选择题

我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数的不足近似值和过剩近似值分别为和（），则是的更为精确的不足近似值或过剩近似值.我们知道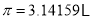，若令，则第一次用“调日法”后得是的更为精确的过剩近似值，即，若每次都取得最简分数，那么第四次用“调日法”后可得的近似数为（）