
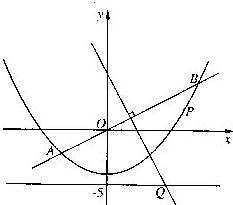
如图,
直线y=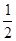 x与抛物线y=
x与抛物线y=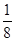 x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.

(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方
(含A、B)的动点时, 求ΔOPQ面积的最大值.
(1) Q(5,-5) (2)ΔOPQ的面积最大值为30
【解析】试题分析:(1) 解方程组  得
得 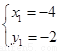 或
或 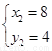
即A(-4,-2),B(8,4), 从而AB的中点为M(2,1).由kAB=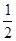 ,直线AB的垂直平分线方程
,直线AB的垂直平分线方程
y-1=-2 (x-2). 令y=-5, 得x=5, ∴Q(5,-5).
(2) 直线OQ的方程为x+y=0, 设P(x, 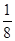 x2-4).∵点P到直线OQ的距离
x2-4).∵点P到直线OQ的距离
d=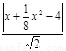 =
=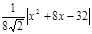 ,
,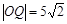 ,∴SΔOPQ=
,∴SΔOPQ=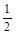
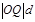 =
=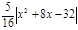 .
.
∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上, ∴-4≤x<4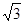 -4或4
-4或4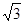 -4<x≤8.
-4<x≤8.
∵函数y=x2+8x-32在区间[-4,8] 上单调递增, ∴当x=8时, ΔOPQ的面积取到最大值30.
考点:抛物线与直线的相交弦问题。
点评:本题(1)比较简单,用一般解决相交弦问题的方法,联立直线与抛物线方程求解即可。(2) 中要考虑到P为抛物线上位于线段AB下方的点,故得-4≤x<4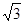 -4或4
-4或4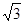 -4<x≤8.转化为求二次函数在闭区间上的最值问题来求。
-4<x≤8.转化为求二次函数在闭区间上的最值问题来求。


科目:高中数学 来源: 题型:
(04年上海卷文)(本题满分14分) 第1小题满分6分, 第2小题满分8分
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方
(含A、B) 的动点时, 求ΔOPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
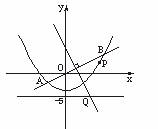 如图, 直线y=
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方(含点A、B)的动点时,求△OPQ面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
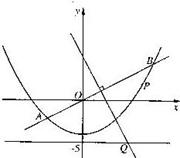 (1) 求点Q的坐标;
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方
(含A、B) 的动点时, 求ΔOPQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com