
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ,
,![]() ”是假命题
”是假命题
C.若命题![]() 、
、![]() 均为假命题,则命题
均为假命题,则命题![]() 为真命题
为真命题
D.若![]() 是定义在R上的函数,则“
是定义在R上的函数,则“![]() ”是“
”是“![]() 是奇函数”的必要不允分条件
是奇函数”的必要不允分条件
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生的选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计选考科目人数如下表:
名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从选考方案确定的![]() 名学生中随机选出
名学生中随机选出![]() 名,试求在选取的
名,试求在选取的![]() 名学生中恰有
名学生中恰有![]() 名男生的条件下两名学生的选考方案中都含有历史学科的概率;
名男生的条件下两名学生的选考方案中都含有历史学科的概率;
(3)从选考方案确定的![]() 名男生中随机选出
名男生中随机选出![]() 名,设随机变量
名,设随机变量![]() 表示所选
表示所选![]() 人中选考方案完全相同的人数(若有
人中选考方案完全相同的人数(若有![]() 组
组![]() 人选考方案完全相同,则
人选考方案完全相同,则![]() ),求
),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形ABCD是直角梯形,
.四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
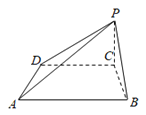
(1)求证:![]() 平面PDC.
平面PDC.
(2)请在图中所给的五个点P,A,B,C,D中找出两个点,使得这两点所在直线与直线BC垂直,并给出证明.
(3)当平面![]() 平面ABCD时,求直线PC与平面PAB所成角的正弦值.
平面ABCD时,求直线PC与平面PAB所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com