
| A. | 2 | B. | $\frac{3}{2}$ | C. | $2\sqrt{3}$ | D. | $\frac{13}{6}$ |
分析 先由a≤$\sqrt{3}$b,及a2=b2+c2,求得椭圆离心率的范围,再利用换元法将函数y=e2+$\frac{1}{e^2}$转化为函数y=t+$\frac{1}{t}$(0<t≤$\frac{2}{3}$),最后利用导数判断此函数的单调性,求出函数的最小值.
解答 解:∵a≤$\sqrt{3}$b,∴a2≤3b2,∴a2≤3(a2-c2),即2a2≥3c2,∴0<e2≤$\frac{2}{3}$
设t=e2,则y=e2+$\frac{1}{{e}^{2}}$=t+$\frac{1}{t}$ (0<t≤$\frac{2}{3}$)
∵y′(t)=1-$\frac{1}{{t}^{2}}$<0,
∴y=t+$\frac{1}{t}$(0<t≤$\frac{2}{3}$)为(0,$\frac{2}{3}$]上的减函数
∴y≥$\frac{2}{3}$+$\frac{1}{\frac{2}{3}}$=$\frac{13}{6}$,即e2+$\frac{1}{e^2}$的最小值为$\frac{13}{6}$
故选:D.
点评 本题考查了椭圆的几何性质离心率的求法,考查特殊函数的单调性和最值的求法,注意本题的函数y=t+$\frac{1}{t}$(0<t≤$\frac{2}{3}$)不适合用均值定理求最值.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3x)′=3xln3 | B. | (x2lnx)′=2xlnx+x | ||
| C. | ($\frac{cosx}{x}$)′=$\frac{xsinx-cosx}{{x}^{2}}$ | D. | (x+$\frac{1}{x}$+$\sqrt{x}$)′=1-$\frac{1}{{x}^{2}}$+$\frac{1}{2\sqrt{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
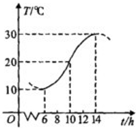 如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.
如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com