
分析 设△ABC中 AB=AC,作AD⊥BC于D,设∠CAD=α,则∠CAB=2α.利用二倍角的余弦公式列式,解出sinα=$\frac{\sqrt{6}}{6}$.进而在Rt△ACD中算出cosC=$\frac{\sqrt{6}}{6}$.
解答 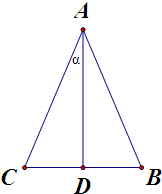 解:设等腰三角形为△ABC,AB=AC,如图所示
解:设等腰三角形为△ABC,AB=AC,如图所示
作AD⊥BC于D,设∠CAD=α,则∠CAB=2α
∵cos∠CAB=$\frac{2}{3}$,即cos2α=$\frac{2}{3}$
∴1-2sin2α=$\frac{2}{3}$,解之得sinα=$\frac{\sqrt{6}}{6}$(舍负)
因此,Rt△ACD中,cos∠C=sinα=$\frac{\sqrt{6}}{6}$,
即此等腰三角形的底角的余弦值等于$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{\sqrt{6}}{6}$.
点评 本题着重考查了二倍角的三角函数公式和解三角形等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
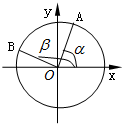 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | (-∞,-1)∪(1,+∞) | C. | $({\frac{1}{2},+∞})$ | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}π$ | B. | $\frac{5}{4}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com