
分析 若x2-y2-3x-3y=(x+y)(x-y-3)=0,则x+y=0,或x-y-3=0,分别代入方程x2-xy+y2=9,消去y,可得满足条件的x值.
解答 解:∵x2-y2-3x-3y=(x+y)(x-y-3)=0,
∴x+y=0,或x-y-3=0,
当x+y=0时,y=-x,
则x2-xy+y2=3x2=9,解得:x=±$\sqrt{3}$,
当x-y-3=0时,y=x-3,
则x2-xy+y2=x2-3x+9=9,解得:x=0,或x=3,
综上所述,实数x的所有取值构成的集合为{-$\sqrt{3}$,0,$\sqrt{3}$,3},
故答案为:{-$\sqrt{3}$,0,$\sqrt{3}$,3}
点评 本题考查的知识点二元二次方程的解法,列举法表示集合,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 1 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
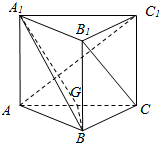 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2<x+1 | B. | ?x∈R,x2≥x+1 | ||
| C. | ?x∈R,?y∈R,xy2=y2 | D. | ?x∈R,?y∈R,x>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com