
【题目】给出下列说法,正确的有__________.
①与![]() 共线单位向量的坐标是
共线单位向量的坐标是![]() ;
;
②集合![]() 与集合
与集合![]() 是相等集合;
是相等集合;
③函数![]() 的图象与
的图象与![]() 的图象恰有3个公共点;
的图象恰有3个公共点;
④函数![]() 的图象是由函数
的图象是由函数![]() 的图象水平向右平移一个单位后,将所得图象在
的图象水平向右平移一个单位后,将所得图象在![]() 轴右侧部分沿
轴右侧部分沿![]() 轴翻折到
轴翻折到![]() 轴左侧替代
轴左侧替代![]() 轴左侧部分图象,并保留右侧部分而得到.
轴左侧部分图象,并保留右侧部分而得到.
【答案】②④
【解析】
与![]() (﹣3,4)共线的单位向量有两个,判定命题①是错误的;
(﹣3,4)共线的单位向量有两个,判定命题①是错误的;
分析出A、B两个集合均表示奇数集,可判断②;
分别画出函数![]() 的图象与y=|x2﹣1|的图象,即可判断③;
的图象与y=|x2﹣1|的图象,即可判断③;
运用函数图象平移变换和对称变换,即可判断④.
对于①,与![]() (﹣3,4)共线的单位向量是(
(﹣3,4)共线的单位向量是(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),
),
∴命题①错误;
②集合![]() 与集合
与集合![]() 均表示奇数集,是相等集合,故②正确;
均表示奇数集,是相等集合,故②正确;
③分别画出函数![]() 的图象与y=|x2﹣1|的图象,
的图象与y=|x2﹣1|的图象,
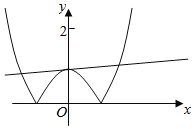
可得x>1和x<﹣1时,各有一个交点;
当﹣1<x<1时,y=1﹣x2和y=1+0.1x,联立可得x2+0.1x=0,
即x=0或x=﹣0.1,则有两个交点;
函数![]() 的图象与y=|x2﹣1|的图象共有4个公共点,故③错误;
的图象与y=|x2﹣1|的图象共有4个公共点,故③错误;
④函数f(|x|﹣1)的图象是由函数f(x)的图象水平向右平移一个单位得到f(x-1)后,
再将所得图象在y轴右侧部分沿y轴翻折到y轴左侧替代y轴左侧部分图象,
并保留右侧部分而得到,故④正确;
综上可得①③错误;②④正确.
故答案为:②④.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益![]() 、养鸡的收益
、养鸡的收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]()
![]() .设甲合作社的投入为
.设甲合作社的投入为![]() (单位:万元).两个合作社的总收益为
(单位:万元).两个合作社的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作的投入,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点![]() ,且与圆M:
,且与圆M:![]() 关于直线
关于直线![]() 对称.
对称.
![]() 求圆C的方程;
求圆C的方程;
![]() 过点P作两条相异直线分别与圆C相交于点A和点B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
过点P作两条相异直线分别与圆C相交于点A和点B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了确定工效,进行了5次试验,收集数据如下:
加工零件个数 | 10 | 20 | 30 | 40 | 50 |
加工时间 | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据的两个变量![]() 与
与![]() 具有线性相关关系,那么对于加工零件的个数
具有线性相关关系,那么对于加工零件的个数![]() 与加工时间
与加工时间![]() 这两个变量,下列判断正确的是( )
这两个变量,下列判断正确的是( )
A. 负相关,其回归直线经过点![]() B. 正相关,其回归直线经过点
B. 正相关,其回归直线经过点![]()
C. 负相关,其回归直线经过点![]() D. 正相关,其回归直线经过点
D. 正相关,其回归直线经过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面ABCD是正方形,
的底面ABCD是正方形,![]() 为等边三角形,M,N分别是AB,AD的中点,且平面
为等边三角形,M,N分别是AB,AD的中点,且平面![]() 平面ABCD.
平面ABCD.

![]() 证明:
证明:![]() 平面PNB;
平面PNB;
![]() 设点E是棱PA上一点,若
设点E是棱PA上一点,若![]() 平面DEM,求
平面DEM,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若把曲线![]() 各点的横坐标伸长到原来的
各点的横坐标伸长到原来的![]() 倍,纵坐标变为原来的
倍,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅲ)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)X表示所取3张卡片上的数字的中位数,求X的分布列与数学期望.(注:若三个数字a,b,c满足a≤b≤c,则称b为这三个数的中位数.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com