
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为
,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为![]() .
.
(1)求椭圆的标准方程;
(2)在C上是否存在点P,使得当L绕F转到某一位置时,有![]() 成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,详见解析.
;(2)存在,详见解析.
【解析】
(1)设![]() ,可得直线L方程为
,可得直线L方程为![]() ,利用点到直线距离公式即可得
,利用点到直线距离公式即可得![]() ,利用离心率即可得
,利用离心率即可得![]() ,再利用
,再利用![]() 求得
求得![]() 后即可得解;
后即可得解;
(2)设![]() ,
,![]() ,则
,则![]() ,按照直线L的斜率是否为0分类,当直线L斜率不为0时,设直线L的方程为
,按照直线L的斜率是否为0分类,当直线L斜率不为0时,设直线L的方程为![]() ,联立方程组结合韦达定理即可得
,联立方程组结合韦达定理即可得![]() 、
、![]() ,将点P坐标代入椭圆方程求得
,将点P坐标代入椭圆方程求得![]() 后即可得解.
后即可得解.
(1) 设![]() ,当L的斜率为1时,其方程为
,当L的斜率为1时,其方程为![]() ,
,
则原点O到直线L的距离为![]() ,解得
,解得![]() ,
,
由椭圆的离心率![]() ,可得
,可得![]() ,
,![]() ,
,
所以椭圆方程为![]() ;
;
(2)假设C上存在点P,使得当L绕F转到某一位置时,有![]() 成立.
成立.
设![]() ,
,![]() ,则
,则![]() ,
,
由(1)知,椭圆C的方程为![]() ,
,
当直线L斜率为0时,点![]() ,不合题意;
,不合题意;
当直线L斜率不为0时,设直线L的方程为![]() ,
,
由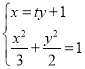 ,消去x化简得
,消去x化简得![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以点![]() ,
,
又因为点![]() 在椭圆上,所以
在椭圆上,所以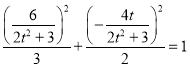 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
当![]() 时,点
时,点 ,直线L的方程为
,直线L的方程为![]() 即
即![]() ;
;
当![]() 时,点
时,点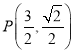 ,直线L的方程为
,直线L的方程为![]() 即
即![]() .
.
综上,椭圆C上存在点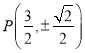 ,使得当L绕F转到某一位置时,有
,使得当L绕F转到某一位置时,有![]() 成立,此时直线方程为
成立,此时直线方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
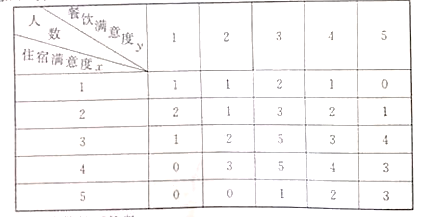
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,![]() .
.
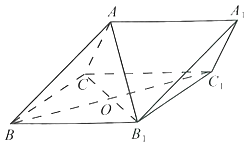
(1)求证:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且点A在侧面BB1C1C上的投影为点O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四面体P-ABC的棱长均为a,O为正四面体P-ABC的外接球的球心,过点O作平行于底面ABC的平面截正四面体P-ABC,得到三棱锥P-A1B1C1和三棱台ABC-A1B1C1,那么三棱锥P-A1B1C1的外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
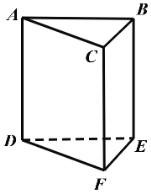
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型科学竞技真人秀节目挑选选手的方式为:不但要对选手的空间感知、照相式记忆能力进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有95%以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,求这11名学生中男、女生人数;若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),分别求这11名学生中女生测试分数平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: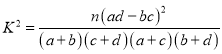 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com