
分析 (1)以十位数为茎,以个位数为叶,能作出茎叶图.
(2)由题意能求出甲、乙的成绩的平均数与方差.
(3)甲乙的平均分一样,证明平均成绩一样,但是甲的方差小于乙的方差,则证明甲的成绩更稳定,由此得到选派甲学生参加合适.
解答 解:(1)以十位数为茎,以个位数为叶,作出茎叶图如右图所示.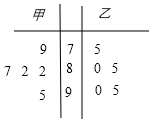
(2)甲的成绩的平均数$\overline{{x}_{甲}}$=$\frac{1}{5}$(82+82+79+95+87)=85,
乙的成绩的平均数$\overline{{x}_{乙}}$=$\frac{1}{5}$(75+95+80+90+85)=85,
甲的方差${{S}_{甲}}^{2}$=$\frac{1}{5}$[(82-85)2+(82-85)2+(79-85)2+(95-85)2+(87-85)2]=31.6,
乙的方差${{S}_{乙}}^{2}$=$\frac{1}{5}$[(75-85)2+(95-85)2+(80-85)2+(90-85)2+(85-85)2]=50.
(3)派甲参赛比较合理.
理由是甲乙的平均分一样,证明平均成绩一样,
但是甲的方差小于乙的方差,则证明甲的成绩更稳定.
点评 本题考查茎叶图、平均数、方差等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是基础题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | 2n-1 | C. | 2×3n-1. | D. | $\frac{1}{2}({{3^n}-1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(x)的最小正周期是π,其图象关于$x=-\frac{π}{4}$对称 | |
| B. | y=f(x)的最小正周期是2π,其图象关于$x=\frac{π}{2}$对称 | |
| C. | y=f(x)的最小正周期是π,其图象关于$x=\frac{π}{2}$对称 | |
| D. | y=f(x)的最小正周期是2π,其图象关于$x=-\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限或第三象限 | B. | 第二象限或第四象限 | ||
| C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
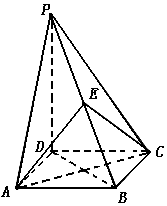 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com