
分析 由题意可知x+y=1,x,y∈[0,1],将y=1-x代入不等式,分理变量,整理得k<$\frac{2{x}^{2}-3x+2}{4-{x}^{2}}$,构造辅助函数,求导根据单调性求得其最小值,即可求得k的取值范围.
解答 解:点C是线段AB上任意一点,O是直线AB外一点,$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$
∴x+y=1,x,y∈[0,1],
将y=1-x代入不等式x2(y+1)+y2(x+2)>k(x+2)(y+1)中,
可得2x2-3x+2>k(4-x2),即k<$\frac{2{x}^{2}-3x+2}{4-{x}^{2}}$,
令f(x)=$\frac{2{x}^{2}-3x+2}{4-{x}^{2}}$,x∈[0,1],对f(x)求导,得f′(x)=$\frac{-3{x}^{2}+20x-12}{(4-{x}^{2})^{2}}$,
令f′(x)>0,解得:$\frac{2}{3}$<x<1,
f′(x)<0,解得:0<x<$\frac{2}{3}$,
∴f(x)在[0,$\frac{2}{3}$]上递减,在[$\frac{2}{3}$,1]上递增,
当x=$\frac{2}{3}$时,f(x)有最小值,
最小值为$\frac{1}{4}$,
所以当k<$\frac{1}{4}$时,不等式恒成立,
故答案为:$(-∞,\frac{1}{4})$.
点评 本题考查向量基本定理及其性质,考查分离变量法求函数的取值范围,利用导数法求函数的单调性及其最值,综合能力强,计算复杂,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
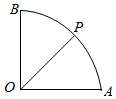 扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )
扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [1,$\sqrt{3}$] | C. | [1,2] | D. | [1,$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
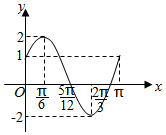 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com