
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由条件,利用三角函数的奇偶性和单调性,得出结论.
解答 解:由于下列函数中,对于函数①y=tan|x|,当x=$\frac{π}{2}$时,函数无意义,故①不满足条件.
对于②y=cos(-x)=cosx为偶函数,且在(0,π)上递减,故②不满足条件.
对于③$y=sin({x-\frac{π}{2}})$=-cosx 为偶函数,且在(0,π)上递增,故③满足条件.
当x∈(0,π)时,$\frac{x}{2}$∈(0,$\frac{π}{2}$),tan$\frac{x}{2}$单调递增,
故$y=|{cot\frac{x}{2}}|$=$\frac{1}{|tan\frac{x}{2}|}$是偶函数,且在(0,π)上递减,故④不满足条件,
故选:A.
点评 本题主要考查三角函数的奇偶性和单调性,属于基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | ${y_1}=\frac{(x+3)(x-5)}{x+3},{y_2}=x-5$ | B. | y1=$\sqrt{x+1}$•$\sqrt{x-1}$,y2=$\sqrt{(x+1)(x-1)}$ | ||
| C. | y1=x,y2=$\sqrt{{x}^{2}}$ | D. | y1=$\root{3}{{x}^{4}-{x}^{3}}$,y2=$x\root{3}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1023 | B. | 1025 | C. | 513 | D. | 511 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
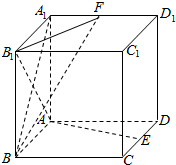 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2) | B. | ($\sqrt{6}$,3) | C. | (3,$\sqrt{6}$) | D. | ($\frac{9}{2}$,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com