
【题目】下面结论中,正确结论的是( )
A.存在两个不等实数![]() ,使得等式
,使得等式![]() 成立
成立
B.![]() (0< x < π)的最小值为4
(0< x < π)的最小值为4
C.若![]() 是等比数列
是等比数列![]() 的前
的前![]() 项的和,则
项的和,则![]() 成等比数列
成等比数列
D.已知![]() 的三个内角
的三个内角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() ,则
,则![]() 一定是锐角三角形
一定是锐角三角形
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,若该项指标值落在[20,40)内的产品视为合格品,否则为不合格品,图1是设备改造前样本的频率分布直方图,表1是设备改造后的频数分布表.

表1,设备改造后样本的频数分布表:
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计该企业在设备改造前的产品质量指标的平均数;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在[25,30)内的定为一等品,每件售价240元,质量指标值落在[20,25)或[30,35)内的定为二等品,每件售价180元,其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X得分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]() ,将
,将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() ,当
,当![]() 时,都有
时,都有![]() ,求实数
,求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求实数
的交点个数不少于6个且不多于10个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
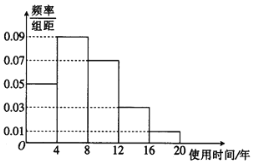
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
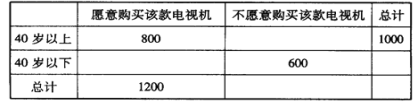
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一湖中有不在同一直线的三个小岛A、B、C,前期为开发旅游资源在A、B、C三岛之间已经建有索道供游客观赏,经测量可知AB两岛之间距离为3公里,BC两岛之间距离为5公里,AC两岛之间距离为7公里,现调查后发现,游客对在同一圆周上三岛A、B、C且位于![]() (优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在
(优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在![]() 上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴顺时针滚动一周,设顶点
轴顺时针滚动一周,设顶点![]() 的运动轨迹与
的运动轨迹与![]() 轴所围区域为
轴所围区域为![]() ,若在平面区域
,若在平面区域![]() 内任意取一点
内任意取一点![]() ,则所取的点
,则所取的点![]() 恰好落在区域
恰好落在区域![]() 内部的概率为
内部的概率为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对每一个实数a,将抛物线![]() 记为
记为![]() 。
。
(1)求所有![]() 的交集;
的交集;
(2)求所有![]() 的焦点的轨迹方程;
的焦点的轨迹方程;
(3)求所有的直线l,使其与所有的![]() 都有公共点;
都有公共点;
(4)求所有的a,使得存在一条以y轴为对称轴且过点![]() 的开口向下的抛物线与
的开口向下的抛物线与![]() 相切。
相切。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com