分析:(Ⅰ)根据等腰直角三角形,可得AM⊥C1M且AM=C1M,根据三垂线定理可知AM⊥CM,而底面ABC为边长为a的正三角形,则即可证得点M为BC边的中点;
(Ⅱ)过点C作CH⊥MC1,根据线面垂直的判定定理可知AM⊥平面C1CM,CH⊥平面C1AM,则CH即为点C到平面AMC1的距离,根据等面积法可求出CH的长;
(Ⅲ)过点C作CI⊥AC1于I,连HI,根据三垂线定理可知HI⊥AC1,根据二面角的平面角的定义可知∠CIH是二面角M-AC1-C的平面角,在直角三角形ACC1中利用等面积法可求出CI,即可求出二面角M-AC1-C的大小.
解答: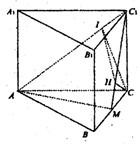
解:(Ⅰ)∵△AMC
1为以点M为直角顶点的等腰直角三角形,
∴AM⊥C
1M且AM=C
1M
∵三棱柱ABC-A
1B
1C
1,∴CC
1⊥底面ABC
∴C
1M在底面内射影为CM,AM⊥CM.
∵底面ABC为边长为a的正三角形,
∴点M为BC边的中点
(Ⅱ)过点C作CH⊥MC
1,由(Ⅰ)知AM⊥C
1M且AM⊥CM,
∴AM⊥平面C
1CM∵CH在平面C
1CM内,
∴CH⊥AM,
∴CH⊥平面C
1AM
由(Ⅰ)知,
AM=CM=a,CM=a且CC1⊥BC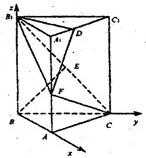
∴
CC1==a∴
CH===a∴点C到平面AMC
1的距离为底面边长为
a(Ⅲ)过点C作CI⊥AC
1于I,连HI,
∵CH⊥平面C
1AM,
∴HI为CI在平面C
1AM内的射影,
∴HI⊥AC
1,∠CIH是二面角M-AC
1-C的平面角,
在直角三角形ACC
1中
CI===a,
sin∠CIH===∴∠CIH=45°,
∴二面角M-AC
1-C的大小为45°
点评:本题主要考查了点线的位置关系,以及点到平面的距离和二面角的度量,同时考查了空间想象能力和计算能力,以及转化与划归的思想,属于中档题.

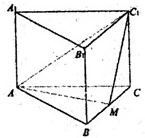 如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形. 解:(Ⅰ)∵△AMC1为以点M为直角顶点的等腰直角三角形,
解:(Ⅰ)∵△AMC1为以点M为直角顶点的等腰直角三角形,


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.