
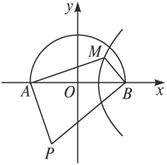
剖析:首先抽象为数学问题,半圆中的点可分为三类:(1)沿AP到P较近;(2)沿BP到P较近;(3)沿AP、BP到P同样远.
显然,第三类点是第一、二类的分界点,设M是分界线上的任意一点.则有|MA|+|PA|=|MB|+|PB|.
于是|MA|-|MB|=|PB|-|PA|=150-100=50.
从而发现第三类点M满足性质:点M到点A与点B的距离之差等于常数50,由双曲线定义知,点M在以A、B为焦点的双曲线的右支上,故问题转化为求此双曲线的方程.
解:以AB所在直线为x轴,线段AB的中点为原点建立直角坐标系xOy,设M(x,y)是沿AP、BP运土同样远的点,则
|MA|+|PA|=|MB|+|PB|,
∴|MA|-|MB|=|PB|-|PA|=50.
在△PAB中,由余弦定理得|AB|2=|PA|2+|PB|2-2|PA||PB|cos60°=17 500,
且50<|AB|.由双曲线定义知M点在以A、B为焦点的双曲线右支上,设此双曲线方程为![]() -
-![]() =1(a>0,b>0).
=1(a>0,b>0).
∵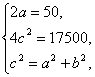
解之得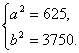
∴M点轨迹是![]() -
-![]() =1(x≥25)在半圆内的一段双曲线弧.于是运土时将双曲线左侧的土沿AP运到P处,右侧的土沿BP运到P处最省工.
=1(x≥25)在半圆内的一段双曲线弧.于是运土时将双曲线左侧的土沿AP运到P处,右侧的土沿BP运到P处最省工.
讲评:(1)本题是不等量与等量关系问题,涉及到分类思想,通过建立直角坐标系,利用点的集合性质,构造圆锥曲线模型(即分界线)从而确定出最优化区域.
(2)应用分类思想解题的一般步骤:①确定分类的对象;②进行合理的分类;③逐类逐级讨论;④归纳各类结果.


科目:高中数学 来源: 题型:
 某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如图所示).已知PA=100 m,PB=150 m,∠APB=60°,试说明怎样运土最省工.
某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如图所示).已知PA=100 m,PB=150 m,∠APB=60°,试说明怎样运土最省工.查看答案和解析>>
科目:高中数学 来源:天骄之路中学系列 读想用 高二数学(上) 题型:044
某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP,BP运到P处(如图所示).|PA|=100米,|PB|=150米,∠APB=60°,试说明怎样运土才能最省工.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
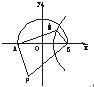 某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如图所示).已知PA=100 m,PB=150 m,∠APB=60°,试说明怎样运土最省工.
某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如图所示).已知PA=100 m,PB=150 m,∠APB=60°,试说明怎样运土最省工.查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:8.6 圆锥曲线的应用(解析版) 题型:解答题
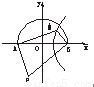
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com