
【题目】如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.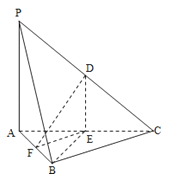
【答案】证明:(1)∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA平面DEF,DE平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE=![]() PA=3;
PA=3;
又∵E、F为AC、AB的中点,∴EF=![]() BC=4;
BC=4;
∴DE2+EF2=DF2 ,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE平面BDE,∴平面BDE⊥平面ABC.
【解析】(1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可.


科目:高中数学 来源: 题型:
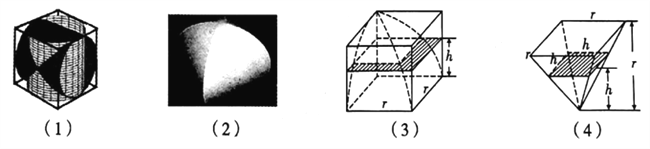
【题目】中国古代数学家刘徽在《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”,如图(1)(2),刘徽未能求得牟合方盖的体积,直言“欲陋形措意,惧失正理”,不得不说“敢不阙疑,以俟能言者”.约200年后,祖冲之的儿子祖暅提出“幂势既同,则积不容异”,后世称为祖暅原理,即:两等高立体,若在每一等高处的截面积都相等,则两立体体积相等.如图(3)(4),祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”,计算出牟合方盖的体积,据此可知,牟合方盖的体积与其外切正方体的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
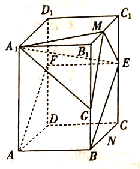
【题目】如图,四边形![]() 是正四棱柱
是正四棱柱![]() 的一个截面,此截面与棱
的一个截面,此截面与棱![]() 交于点
交于点![]() ,
, ![]() ,其中
,其中![]() 分别为棱
分别为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,若四面体
上一点,若四面体![]() 与四棱锥
与四棱锥![]() 的体积相等,求
的体积相等,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中,
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF.
(2)当BE=BF=![]() BC时,求三棱锥A′﹣EFD体积.
BC时,求三棱锥A′﹣EFD体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(﹣x)一定是偶函数;
②若对任意x∈R都有f(x)+f(2﹣x)=0,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对于任意x∈R,都有f(x)+f(2+x)=0,则f(x)的图象的对称轴方程为x=2n+1(n∈Z);
④对于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,则f(x)为R上的增函数,
>0恒成立,则f(x)为R上的增函数,
其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中![]() 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com