
| 2 | ||
|
| 2 | ||
|
2
| ||
| 3 |
| 1 |
| sin60° |
| x |
| sinA |
| y |
| sinB |
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
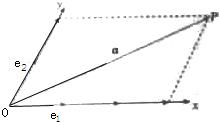 如图,设Ox、Oy是平面内相交成60°角的两条数轴,
如图,设Ox、Oy是平面内相交成60°角的两条数轴,| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OP |
| e1 |
| e2 |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2分球 | 3分球 | |
| 第1场 | 10投5中 | 4投2中 |
| 第2场 | 13投5中 | 5投2中 |
| 第3场 | 8投4中 | 3投1中 |
| 第4场 | 9投5中 | 3投0中 |
| 第5场 | 10投6中 | 6投2中 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.
如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.查看答案和解析>>
科目:高中数学 来源: 题型:
A、若x≠0,则x+
| ||
| B、命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1且x≠-1,则x2≠1 | ||
| C、“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 | ||
| D、若命题P:?x∈R,x2-x+1<0,则¬P:?x∈R,x2-x+1>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com