练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知A，B两地位于北纬45°的纬线上，且两地的经度之差为90°，设地球的半径为Rkm，则时速为20km的轮船从A地到B地，最少需要的小时数是（ ）
    A．
    B．
    C．
    D．
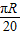
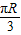    【答案】分析：设北纬45°纬线的小圆圆心为Q，算出△AOB是等边三角形，得∠AOB=60°，从而得到甲、乙两地的球面距离为，结合轮船的时速为20km即可算出最少需要的小时数．
    解答：解：如图，设北纬45°纬线的小圆圆心为Q
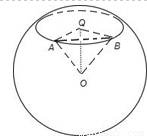    由题意知：∠QAO=∠QBO=45°，∠AQB=90°，
    ∴△QAB≌△QAO
    可得AB=AO=BO=Rkm
    ∴△AOB是等边三角形，得∠AOB=60°，
    得到甲、乙两地的最短距离即球面距离为：s==
    因此，时速为20km的轮船从A地到B地，最少需要t===
    故选：D
    点评：本题给出实际应用问题，求轮船从A地到B地最少需要的小时数．着重考查了球面距离的计算及其实际应用等知识，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

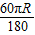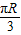
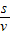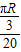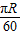
    科目：高中数学 来源： 题型：

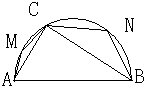    精英家教网已知 A、B两地相距2R，以AB为直径作一个半圆，在半圆上取一点C，连接AC、BC，在三角形ABC内种草坪（如图），M、N分别为弧AC、弧BC的中点，在三角形AMC、三角形BNC上种花，其余是空地．设花坛的面积为S1，草坪的面积为S2，取∠ABC=θ．
    （1）用θ及R表示S1和S2；
    （2）求
    S1S2
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A，B两地相距200km，一只船从A地逆流行驶到B地，水流速为8km/h，船在静水中的速度为vkm/h，（8＜v≤20），若船每小时的燃料费与在静水中的速度的平方成正比，当v=12km/h时，每小时燃料费为720元．
    （1）设船每小时的燃料费为L，求L与v的关系式；
    （2）为了使全程燃料费最省，船的实际速度为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A，B两地位于北纬45°的纬线上，且两地的经度之差为90°，设地球的半径为Rkm，则时速为20km的轮船从A地到B地，最少需要的小时数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A、B两地位于北纬α的纬线上，且两地的经度差为90°，若地球的半径为R千米，且时速为20千米的轮船从A地到B地最少需要
    πR
    60
    小时，则α为（　　）
    A、
    π
    6
    B、
    π
    4
    C、
    π
    3
    D、
    5
    12
    π

    查看答案和解析>>

    同步练习册答案