
【题目】已知椭圆C: ![]() 过点A(2,3),且F(2,0)为其右焦点.
过点A(2,3),且F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在于行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于 ![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】
(1)解:∵椭圆C: ![]() 过点A(2,3),且F(2,0)为其右焦点,
过点A(2,3),且F(2,0)为其右焦点,
∴椭圆C的左焦点为F′(﹣2,0),则|AF|=3,|AF′|= ![]() =5,
=5,
∴ ![]() ,即
,即 ![]() ,∴b2=16﹣4=12,
,∴b2=16﹣4=12,
∴椭圆C的方程为 ![]() =1.
=1.
(2)解:设存在符合题意的直线l,其方程为y= ![]() ,
,
由 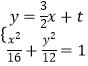 ,整理,得3x2+3tx+t2﹣12=0,
,整理,得3x2+3tx+t2﹣12=0,
∵直线l与椭圆C有公共点,
∴△=(3t)2﹣12(t2﹣12)=﹣3t2+144≥0,
解得﹣4 ![]() ,
,
∵直线OA与l的距离等于 ![]() ,∴
,∴ ![]() =
= ![]() ,故t=±5.
,故t=±5.
∵±5∈[﹣4 ![]() ,4
,4 ![]() ],
],
∴直线l的方程为y= ![]() 或y=
或y= ![]()
【解析】(1)利用椭圆焦点和椭圆定义,求出a,b,由此能求出椭圆C的方程.(2)设存在符合题意的直线l,其方程为y= ![]() ,与椭圆联立,得3x2+3tx+t2﹣12=0,由此利用根的判别式、点到直线的距离公式,能求出结果方程.
,与椭圆联立,得3x2+3tx+t2﹣12=0,由此利用根的判别式、点到直线的距离公式,能求出结果方程.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高,则自服药那一刻起,心率关于时间的一个可能的图象是( )
A.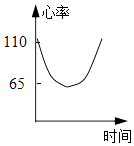
B.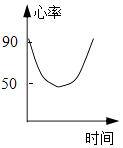
C.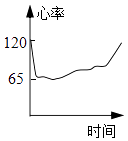
D.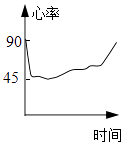
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* .
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=ax上一点M(4,b)到焦点的距离为6.
(1)求抛物线的方程;
(2)若此抛物线与直线y=kx﹣2交于不同的两点A、B,且AB中点的横坐标为2,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点,且PA=AD. 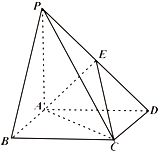
(1)求证:PB∥平面AEC;
(2)求证:AE⊥平面PCD;
(3)设二面角D﹣AE﹣C为60°,且AP=1,求D到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点 
(1)求证:DE∥平面ABC;
(2)求三棱锥E﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC、SC于D、E,又SA=AB,SB=BC, 
(1)求证:BD⊥平面SAC;
(2)求二面角E﹣BD﹣C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com