
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点,且PA=AD. 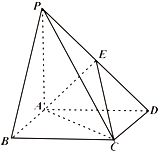
(1)求证:PB∥平面AEC;
(2)求证:AE⊥平面PCD;
(3)设二面角D﹣AE﹣C为60°,且AP=1,求D到平面AEC的距离.
【答案】
(1)证明:连接BD交AC于O点,则O为BD的中点,连结OE,
∵E为PD的中点,∴PB∥OE
又∵OE平面AEC,PB平面AEC
∴PB∥平面AEC;

(2)证明:(几何法):∵PA⊥平面ABCD,
∴PA⊥AD,PA⊥CD
∴在直角△PAD中,PA=ADE为PD的中点,
∴AE⊥PD
又∵底面ABCD为矩形,∴AD⊥CD,
∵PA∩AD=A,∴CD⊥平面PAD
∵AE平面PAD,∴AE⊥CD,∵PD∩CD=D,
∴AE⊥平面PCD.
(向量法):由题知 四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
如图以A点为原点,以AB,AD,AP所在直线分别为x,y,z轴,建立空间坐标系A﹣xyz
设AB=a,AD=b,则 ![]()
∴ ![]() ,
,
∴ ![]() )
)
∴AE⊥DC,AE⊥DP,
∵DP∩DC=D,∴AE⊥平面PCD
(3)解:由(2)知平面DAE的法向量是 ![]() ,
,
∵AP=1,∴ ![]() ,
,
∴ ![]() ,
,
设平面AEC的法向量是 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,令z=1,得
,令z=1,得 ![]() ,∴
,∴ ![]()
∴  ,
,
解得 ![]()
∵ ![]() ,
,
∴D到平面AEC的距离 ![]()
【解析】(1)连接BD交AC于O点,则O为BD的中点,从而PB∥OE,由此能证明PB∥平面AEC.(2)(几何法):推导出PA⊥AD,PA⊥CD,从而AE⊥PD,再推导出AD⊥CD,从而CD⊥平面PAD,进而AE⊥CD,由此能证明AE⊥平面PCD.(2)(向量法):以A点为原点,以AB,AD,AP所在直线分别为x,y,z轴,建立空间坐标系A﹣xyz,利用向量法能证明AE⊥平面PCD.(3)求出平面DAE的法向量和平面AEC的法向量,利用向量法能求出D到平面AEC的距离.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 ![]() .
.
(1)求椭圆C的方程;
(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.
①若线段AB中点的横坐标为﹣ ![]() ,求斜率k的值;
,求斜率k的值;
②若点M(﹣ ![]() ,0),求证:
,0),求证: ![]()
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 过点A(2,3),且F(2,0)为其右焦点.
过点A(2,3),且F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在于行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于 ![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).
(1)该生态园从第几年开始盈利?
(2)该生态园前几年的年平均利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假
B.命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆”
C.命题“若k<9,则方程“ ![]() +
+ ![]() =1表示双曲线”是假命题
=1表示双曲线”是假命题
D.命题“在△ABC中,若sinA< ![]() ,则A<
,则A< ![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,设
命题p:函数y=logax在区间(0,+∞)内单调递减;
q:曲线y=x2+(2a﹣3)x+1与x轴有两个不同的交点,
如果p∧q为真命题,试求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com