
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.分析 (1)根据抛物线y=ax2+bx-4与x轴交于点A(-2,0),且直线x=1是该抛物线的对称轴,构造关于a,b的方程,解得抛物线的解析式;
(2)△APH的面积S=$\frac{1}{2}$AH•PM,分当0<t≤2时和当2<t≤3时两种情况分别讨论S的最大值,综合讨论结果,可得答案.
解答  解:(1)∵抛物线y=ax2+bx-4与x轴交于点A(-2,0),且直线x=1是该抛物线的对称轴.
解:(1)∵抛物线y=ax2+bx-4与x轴交于点A(-2,0),且直线x=1是该抛物线的对称轴.
∴$\left\{\begin{array}{l}4a-2b-4=0\\-\frac{b}{2a}=1\end{array}\right.$,
解得:a=$\frac{1}{2}$,b=-1,
∴抛物线的解析式为y=$\frac{1}{2}$x2-x-4;
(2)令$\frac{1}{2}$x2-x-4=0,得x=-2,或x=4,
故B点坐标为(4,0),
令x=0,则$\frac{1}{2}$x2-x-4=-4,
故C点坐标为(0,-4),
∴OB=OC=4,AB=6,
∴∠OBC=45°,
如图1:
当0<t≤2时,
∵PM∥OC,
∴AM:OA=PM:OC,
∴t:2=PM:4,即PM=2t,
∵BH=t,
∴AH=6-t,
∴△APH的面积S=$\frac{1}{2}$AH•PM=$\frac{1}{2}$(6-t)2t=-t2+6t,
当t=2时,S取最大值8;
如图2:
当2<t≤3时,
BH=2-(t-2)×$\frac{3}{2}$=5-$\frac{3}{2}$t,
∴AH=6-BH=1+$\frac{3}{2}$t,
∵AM=t,
∴BM=6-t,
∴△APH的面积S=$\frac{1}{2}$AH•PM=$\frac{1}{2}$(1+$\frac{3}{2}$t)(6-t)=-$\frac{3}{4}$t2+4t+3,
当t=$\frac{8}{3}$时,S取最大值$\frac{25}{3}$;
综上所述:S的最大值为$\frac{25}{3}$;
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{78}{71}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
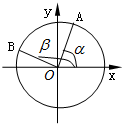 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}π$ | B. | $\frac{5}{4}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com