
【题目】已知数列![]() 和
和![]() 都是等差数列,
都是等差数列,![]() .数列
.数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)证明:![]() 是等比数列;
是等比数列;
(3)是否存在首项为1,公比为q的等比数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立?若存在,求出q的取值范围;若不存在,请说明理由.
成立?若存在,求出q的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在,
;(2)证明见解析;(3)存在,![]() .
.
【解析】
(1)设![]() 的公差为d,可得
的公差为d,可得![]() ,
,![]() , 由
, 由![]() 是等差数列,可得
是等差数列,可得![]() 成等差数列,可得
成等差数列,可得![]() ,求出
,求出![]() 的值,可得
的值,可得![]() 的通项公式;
的通项公式;
(2)将![]() 展开,可得
展开,可得![]() ,将
,将![]() 代入此式子相减,可得
代入此式子相减,可得![]() ,再将
,再将![]() 代入此式子相减,可得
代入此式子相减,可得![]() ,此时
,此时![]() ,验证
,验证![]() 时也满足可得
时也满足可得![]() 是等比数列;
是等比数列;
(3)设存在![]() 对任意
对任意![]() ,都有
,都有![]() 恒成立,即
恒成立,即![]() ,
,![]() ,易得
,易得![]() ,由由
,由由![]() 得,
得,![]() ,可得设
,可得设![]() ,对其求导,可得其最小值,可得q的取值范围.
,对其求导,可得其最小值,可得q的取值范围.
解:(1)因为数列![]() 是等差数列,设
是等差数列,设![]() 的公差为d,则
的公差为d,则
![]() ,
,![]() ,
,
因为![]() 是等差数列,所以
是等差数列,所以![]() 成等差数列,
成等差数列,
即![]() ,
,![]() ,
,
解得![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 是等差数列.
是等差数列.
故![]() .
.
(2)由![]() ,即
,即![]() , ①
, ①
所以![]() , ②
, ②
②-①得,![]() , ③
, ③
所以,![]() , ④
, ④
④-③得,![]() ,即
,即![]() 时,
时,![]() ,
,
在①中分别令![]() 得,
得,![]() ,也适合上式,
,也适合上式,
所以![]() ,
,![]() ,
,
因为![]() 是常数,所以
是常数,所以![]() 是等比数列.
是等比数列.
(3)设存在![]() 对任意
对任意![]() ,都有
,都有![]() 恒成立,
恒成立,
即![]() ,
,![]() ,
,
显然![]() ,由
,由![]() 可知,
可知,![]() ,
,
由![]() 得,
得,![]() ,
,![]() .
.
设![]() ,因为
,因为![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 递增;
递增;
当![]() 时,
时,![]() ,
,![]() 递减.
递减.
因为![]() ,所以
,所以![]() ,
,
解得![]() ,
,
综上可得,存在等比数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 恒成立, 其中公比
恒成立, 其中公比![]() 的取值范围是
的取值范围是![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为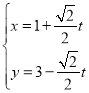 (
(![]() 为参数且
为参数且![]() ).在以坐标原点为极点,
).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求证:
上,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:
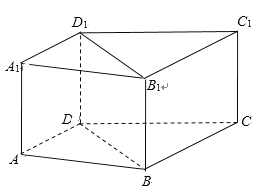
(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人某天的工作是:驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() 三地之间各路段行驶时间及当天降水概率如表:
三地之间各路段行驶时间及当天降水概率如表:
路段 | 正常行驶所需时间(小时) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,则在该路段行驶的时间需延长1小时,现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事,然后到达
地办事,然后到达![]() 地,下午在
地,下午在![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地, 办事后返回
地, 办事后返回![]() 地.
地.
(1)设此人8点从![]() 地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率;
地的概率;
(2)甲、乙两个方案中,哪个方案有利于办完事后能更早返回![]() 地?
地?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后,某科技企业为抓住“一带一路”带来的机遇,决定开发生产一款大型电子设备.生产这种设备的年固定成本为500万元,每生产x台,需另投入成本![]() 万元
万元![]() ,当年产量不足60台时,
,当年产量不足60台时,![]() 万元
万元![]() ;当年产量不小于60台时,
;当年产量不小于60台时,![]() 万元
万元![]() 若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.
若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.
![]() 求年利润
求年利润![]() 万元
万元![]() 关于年产量
关于年产量![]() 台
台![]() 的函数关系式;
的函数关系式;
![]() 当年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?
当年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 截直线
截直线![]() 所得的线段的长度为
所得的线段的长度为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com