练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，直线的参数方程为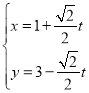（为参数且）．在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为．

    （1）求直线的极坐标方程及曲线的直角坐标方程；

    （2）若点在直线上，点在曲线上，求证：．

    【答案】（1），；（2）证明见解析.

    【解析】

    （1）先将直线的参数方程化为普通方程，再将直线的普通方程转化为极坐标方程，利用可将曲线的极坐标方程转化为直角坐标方程；

    （2）设点的坐标为，利用点到直线的距离公式以及三角函数的有界性可证明出.

    （1）在直线的参数方程（为参数且）中消去参数得，所以，直线的极坐标方程为.

    曲线的极坐标方程为，即，即，

    转化为直角坐标方程为，即；

    （2）曲线的参数方程为（为参数），

    设点的坐标为，则点到直线的距离为，

    因此，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了让贫困地区的孩子们过一个温暖的冬天，某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动，共有50名志愿者参与.志愿者的工作内容有两项：①到各班做宣传，倡议同学们积极捐献冬衣；②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况，只参与其中的某一项工作.相关统计数据如下表所示：

    （1）如果用分层抽样的方法从参与两项工作的志愿者中抽取5人，再从这5人中选2人，那么“至少有1人是参与班级宣传的志愿者”的概率是多少？

    （2）若参与班级宣传的志愿者中有12名男生，8名女生，从中选出2名志愿者，用表示所选志愿者中的女生人数，写出随机变量的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数的最大值；

    （2）若函数与有相同极值点．

    ①求实数的值；

    ②若对于（为自然对数的底数），不等式恒成立，

    求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，设.

    （Ⅰ）若在处取得极值，且，求函数的单调区间；

    （Ⅱ）若时函数有两个不同的零点、.

    ①求的取值范围；②求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求函数的极值点；

    （2）设函数有两个零点，求整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：的左焦点为，且点在C上．

    求C的方程；

    设点P关于x轴的对称点为点不经过P点且斜率为k的直线l与C交于A，B两点，直线PA，PB分别与x轴交于点M，N，若，求k．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面外ABC的一点P，AP、AB、AC两两互相垂直，过AC的中点D做ED⊥面ABC，且ED=1，PA=2，AC=2，连接BP，BE，多面体B﹣PADE的体积是；

    （1）画出面PBE与面ABC的交线，说明理由；

    （2）求面PBE与面ABC所成的锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列和都是等差数列，.数列满足.

    （1）求的通项公式；

    （2）证明：是等比数列；

    （3）是否存在首项为1，公比为q的等比数列，使得对任意，都有成立？若存在，求出q的取值范围；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过两点，且圆心在直线上.

    （Ⅰ）求圆的标准方程；

    （Ⅱ）设直线经过点，且与圆相交所得弦长为，求直线的方程.

    查看答案和解析>>

    同步练习册答案