
【题目】设函数![]() .
.
(1)求函数![]() 的极值点;
的极值点;
(2)设函数![]() 有两个零点,求整数
有两个零点,求整数![]() 的最小值.
的最小值.
【答案】(1)![]() 的极大值点为0(2)2
的极大值点为0(2)2
【解析】
(1)对![]() 求导,
求导,![]() ,因为
,因为![]() 恒大于
恒大于![]() ,所以
,所以![]() 的正负等价于
的正负等价于![]() 的正负,构造新的函数,求导判断
的正负,构造新的函数,求导判断![]() 的正负,从而求出
的正负,从而求出![]() 的极值点;
的极值点;
(2)将![]() 的零点问题转化为函数
的零点问题转化为函数![]() 与函数
与函数![]() 图像的交点问题,判断
图像的交点问题,判断![]() 的极大值的范围,构造关于
的极大值的范围,构造关于![]() 的极大值的函数,利用导数求得其范围,从而得到
的极大值的函数,利用导数求得其范围,从而得到![]() 的范围,求出整数
的范围,求出整数![]() 的最小值.
的最小值.
因为![]() ,
,
令![]() ,
,![]() ,
,
因为当![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上为减函数,
上为减函数,
因为![]() ,又因为
,又因为![]() 在
在![]() 上为减函数.
上为减函数.
当![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 为增函数,
为增函数,
当![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 为减函数,
为减函数,
所以![]() 的极大值点为0.
的极大值点为0.
(2)![]() ,
,
由题意函数![]() 有两个零点,
有两个零点,
可转化为函数![]() 与函数
与函数![]() 的图像有两个交点,
的图像有两个交点,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
即![]() 在
在![]() 上为减函数,
上为减函数,
因为![]() ,
,![]() ,
,
![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 为增函数,
为增函数,
当![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 为减函数,
为减函数,
![]() ,
,
由![]() 得
得![]() ,所以
,所以![]() ,
,
代入得![]() ,
,
事实上![]() ,
,![]() ,即
,即![]() ,
,
令![]() ,
,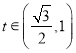 ,
,![]() ,
,
带入![]() 化简得
化简得
![]() ,
,
又因为![]() 在区间
在区间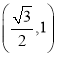 为减函数,
为减函数,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
所以整数![]() 的最小值为2.
的最小值为2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生![]() 和
和![]() 都不是第一个出场,
都不是第一个出场,![]() 不是最后一个出场”的前提下,学生
不是最后一个出场”的前提下,学生![]() 第一个出场的概率为( )
第一个出场的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功,每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为![]() ,
,![]() ,
,![]() ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用![]() 表示小王所获得获品的价值,写出
表示小王所获得获品的价值,写出![]() 的概率分布列,并求
的概率分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱,1个单位的固体碱在水中逐步溶化,水中的碱浓度![]() 与时间
与时间![]() 的关系,可近似地表示为
的关系,可近似地表示为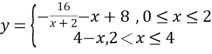 ,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为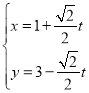 (
(![]() 为参数且
为参数且![]() ).在以坐标原点为极点,
).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求证:
上,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 求曲线
求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若射线l:
若射线l:![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为A,
的交点分别为A,![]() B异于原点
B异于原点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:
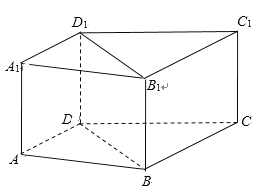
(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市新上一种瓶装洗发液,为了打响知名度,举行为期六天的低价促销活动,随着活动的有效开展,第六天该超市对前五天中销售的洗发液进行统计,y表示第x天销售洗发液的瓶数,得到统计表格如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 4 | 6 | 10 | 15 | 20 |
(1)若y与x具有线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并预测第六天销售该洗发液的瓶数(按四舍五入取到整数);
,并预测第六天销售该洗发液的瓶数(按四舍五入取到整数);
(2)超市打算第六天加大活动力度,购买洗发液可参加抽奖,中奖者可领取奖金20元,中奖概率为![]() ,已知甲、乙两名顾客抽奖中奖与否相互独立,求甲、乙所获得奖金之和X的分布列及数学期望.
,已知甲、乙两名顾客抽奖中奖与否相互独立,求甲、乙所获得奖金之和X的分布列及数学期望.
参考公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com