
【题目】平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B﹣PADE的体积是![]() ;
;

(1)画出面PBE与面ABC的交线,说明理由;
(2)求面PBE与面ABC所成的锐二面角的大小.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为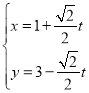 (
(![]() 为参数且
为参数且![]() ).在以坐标原点为极点,
).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求证:
上,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 求曲线
求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若射线l:
若射线l:![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为A,
的交点分别为A,![]() B异于原点
B异于原点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:
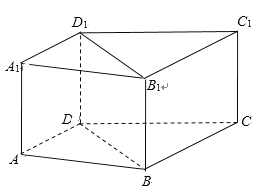
(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后,某科技企业为抓住“一带一路”带来的机遇,决定开发生产一款大型电子设备.生产这种设备的年固定成本为500万元,每生产x台,需另投入成本![]() 万元
万元![]() ,当年产量不足60台时,
,当年产量不足60台时,![]() 万元
万元![]() ;当年产量不小于60台时,
;当年产量不小于60台时,![]() 万元
万元![]() 若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.
若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.
![]() 求年利润
求年利润![]() 万元
万元![]() 关于年产量
关于年产量![]() 台
台![]() 的函数关系式;
的函数关系式;
![]() 当年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?
当年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,
,![]() ,M是椭圆E上的一个动点,且
,M是椭圆E上的一个动点,且![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆E的标准方程,
(2)若![]() ,
,![]() ,四边形ABCD内接于椭圆E,
,四边形ABCD内接于椭圆E,![]() ,记直线AD,BC的斜率分别为
,记直线AD,BC的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com