Question

某学校高一年级组建了A、B、C、D四个不同的“研究性学习”小组，要求高一年级学生必须参加，

且只能参加一个小组的活动．假定某班的甲、乙、丙三名同学对这四个小组的选择是等可能的.

（1）求甲、乙、丙三名同学选择四个小组的所有选法种数；

（2）求甲、乙、丙三名同学中至少有二人参加同一组活动的概率；

（3）设随机变量X为甲、乙、丙三名同学参加A小组活动的人数，求X的分布列与数学期望EX．

 

Answer 1

（1）; （2）; (3)分布列见解析，期望为.

【解析】

试题分析：（1）利用分布乘法原理三名同学先后选择共有种；（2）找出三名同学中至少有二人参加同一组活动的对立面，三名同学选择三个小组的概率为，则可得所求概率为 ;(3)X的可能取值为0，1，2，3，分别求出所对应的概率，列出分布列，进一步求出期望.

【解析】
（1）甲、乙、丙三名同学每人选择四个小组的方法是4种，故有种．（4分）

（2）甲、乙、丙三名同学选择三个小组的概率为，

所以三名同学至少有二人选择同一小组的概率为． （8分）

（3）由题意X的可能取值为：0，1，2，3

，，

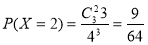，， （12分）

所以X的分布列如下：

X	0	1	2	3
P

 

故数学期望． （14分）

考点：1.排列组合；2.离散型随机变量的分布列与期望.