练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．方程22x-1=$\frac{1}{4}$的解x=-$\frac{1}{2}$．

    分析 原方程转化为22x-1=2-2，根据指数函数的性质得到2x-1=-2，解得即可．

    解答 解：22x-1=$\frac{1}{4}$=2-2，
    ∴2x-1=-2，
    解得x=-$\frac{1}{2}$，
    故答案为：-$\frac{1}{2}$

    点评 本题考查了指数方程的解法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

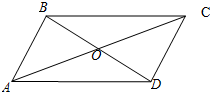    5．如图，在平行四边形ABCD中，BD，AC相交于点O，设向量$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$．
    （1）若AB=1，AD=2，∠BAD=60°，证明：$\overrightarrow{AB}⊥\overrightarrow{BD}$；
    （2）若点P是平行四边形ABCD所在平面内一点，且满足5$\overrightarrow{AP}=\overrightarrow{AC}+3\overrightarrow{AD}$，求△ACP与△ACD的面积的比；
    （3）若AB=AD=2，∠BAD=60°，点E，F分别在边AD，CD上，$\overrightarrow{AE}=λ\overrightarrow{AD}$，$\overrightarrow{CF}=μ\overrightarrow{CD}$，且$\overrightarrow{BE}•\overrightarrow{BF}=1，\overrightarrow{DE}•\overrightarrow{DF}=-\frac{2}{3}$，求λ+μ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．一张长方形白纸，其厚度为a，面积为b，现将此纸对折（沿对边中点连线折叠）5次，这时纸的厚度和面积分别为（　　）
    A．$\frac{1}{32}$a，32bB．32a，$\frac{1}{32}b$C．16a，$\frac{1}{32}b$D．16a，$\frac{1}{16}b$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

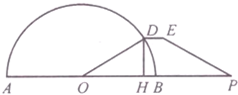    3．如图，AB是半径为r的半圆形广场的直径，在AB的延长线上一点P处，有一停车场，且BP=r，D为半圆上（靠近停车场一侧）的一点，在点D和P之间修建一条折线形道路DEP，已知DE∥BP，并且DE的长等于点D到AB距离DH的一半，设∠BOD=θ（O为半圆的圆心），f（θ）=$\frac{HP}{DE}$．
    （1）求函数f（θ）的解析式；
    （2）求f（θ）的最小值及对应的θ值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若多项式x3+x10=a0+a1（x+1）+…+a9（x+1）9+a10（x+1）10，则a2=42．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图，在△ABC中，若$\overrightarrow{BE}$=2$\overrightarrow{EA}$，$\overrightarrow{AD}$=2$\overrightarrow{DC}$，$\overrightarrow{DE}$=λ（$\overrightarrow{CA}$-$\overrightarrow{BC}$），则实数λ=$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=2sin2（$\frac{π}{4}$+x）-$\sqrt{3}$cos2x
    （1）求函数f（x）的最大值，以及取到最大值时所对应的x的集合；
    （2）|f（x）-m|＜2在x∈[$\frac{π}{4}$，$\frac{π}{2}$]上恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．一物体在力F（x）=2x+1（力的单位：N）的作用下，沿着与力F相同的方向，从x=0处运动到x=3处（单位：m），则力F（x）所作的功为12J．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．倾斜角为$\frac{3π}{4}$且经过点P（1，-2）的直线l的方程为x+y+1=0．

    查看答案和解析>>

    同步练习册答案