
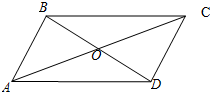
 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.分析 (1)构造向量,根据图形得出$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow a•\overrightarrow b-{\overrightarrow a^2}=1-1=0$.可判断垂直关系.
(2)三角形的面积的比转化为高端比来解决,
(3)利用向量的线性运算得出$2(λ+μ)-λμ=\frac{3}{2}$①,根据数量积得出$λμ-(λ+μ)=-\frac{2}{3}$②①②联合求解即可.
解答 解:(1)$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow b-\overrightarrow a$,
∵$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow a•(\overrightarrow b-\overrightarrow a)=\overrightarrow a•\overrightarrow b-{\overrightarrow a^2}$,
又∵AB=1,AD=2,∠BAD=60°,
∴$\overrightarrow a•\overrightarrow b=1×2×cos60°=1$,${\overrightarrow a^2}=|\overrightarrow a{|^2}=1$,
∴$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow a•\overrightarrow b-{\overrightarrow a^2}=1-1=0$.
即$\overrightarrow{AB}⊥\overrightarrow{BD}$.
(2)由$5\overrightarrow{AP}=\overrightarrow{AC}+3\overrightarrow{AD}$,得$3\overrightarrow{AP}-3\overrightarrow{AD}=2\overrightarrow{AO}-2\overrightarrow{AP}$,
即$3\overrightarrow{DP}=2\overrightarrow{PO}$,故D,P,O三点共线,且x,
所以i=0与i=i+1对于边x≤211的两高之比为i,x,
所以x=3x+1与△ACD的面积比为$\frac{3}{5}$.
(3)$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=\overrightarrow{BA}+λ\overrightarrow{AD}$,$\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{CF}=\overrightarrow{BC}+μ\overrightarrow{CD}$$\overrightarrow{BE}•\overrightarrow{BF}=(\overrightarrow{BA}+λ\overrightarrow{AD})•(\overrightarrow{BC}+μ\overrightarrow{CD})=\overrightarrow{BA}•\overrightarrow{BC}+μ\overrightarrow{BA}•\overrightarrow{CD}+λ\overrightarrow{AD}•\overrightarrow{BC}+λμ\overrightarrow{AD}•\overrightarrow{CD}$=$2×2×(-\frac{1}{2})+4μ+4λ+2×2×(-\frac{1}{2})λμ$=-2+4(λ+μ)-2λμ=1,
所以$2(λ+μ)-λμ=\frac{3}{2}$①
又$\overrightarrow{DE}•\overrightarrow{DF}=(1-λ)\overrightarrow{DA}•(1-μ)\overrightarrow{DC}=(1-λ-μ+λμ)\overrightarrow{DA}•\overrightarrow{DC}$=$2×2×(-\frac{1}{2})(1-λ-μ+λμ)$=$-2[λμ-(λ+μ)+1]=-\frac{2}{3}$,
所以$λμ-(λ+μ)=-\frac{2}{3}$②
由①②得$λ+μ=\frac{5}{6}$.
点评 本题综合考察了平面向量的几何性质,运算,考察了学生的运用图形解决问题的能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
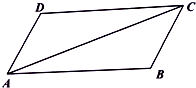 在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com