
 现需要设计一个仓库,它的上部是底面圆半径为5米的圆锥,下部是底面圆半径为5米的圆柱,且该仓库的总高度为5米.经过预算,制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为4百元/米2、1百元/米2.
现需要设计一个仓库,它的上部是底面圆半径为5米的圆锥,下部是底面圆半径为5米的圆柱,且该仓库的总高度为5米.经过预算,制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为4百元/米2、1百元/米2.分析 (1)①由题可知,圆柱的高为x米,且x∈(0,5),利用制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为4百元/米2、1百元/米2,可将y表示为关于x的函数y=f(x);
②设圆锥母线与其轴所在直线所成角为θ,即可将y表示为关于θ的函数y=g(θ);
(2)由②,令$h(θ)=\frac{2-cosθ}{sinθ}$,${h^'}(θ)=\frac{1-2cosθ}{{si{n^2}θ}}=0$,确定函数的单调性,即可得出结论.
解答 解:(1)①由题可知,圆柱的高为x米,且x∈(0,5),…(2分)
则该仓库的侧面总造价$y=(2π×5x)×1+[{\frac{1}{2}×2π×5×\sqrt{(5-x{)^2}+25}}]×4$=$10πx+20π\sqrt{{x^2}-10x+50}$,x∈(0,5)…(4分)
②由题可知,圆锥母线与轴所在直线所成角为θ,且$θ∈({\frac{π}{4},\frac{π}{2}})$,…(6分)
则该仓库的侧面总造价$y=[{2π×5×5(1-\frac{1}{tanθ})}]×1+[{\frac{1}{2}×2π×5×\frac{5}{sinθ}}]×4$=$50π({1+\frac{2-cosθ}{sinθ}})$,$θ∈({\frac{π}{4},\frac{π}{2}})$…(8分)
(2)由②,令$h(θ)=\frac{2-cosθ}{sinθ}$,${h^'}(θ)=\frac{1-2cosθ}{{si{n^2}θ}}=0$得$cosθ=\frac{1}{2}$,$θ∈({\frac{π}{4},\frac{π}{2}})$即$θ=\frac{π}{3}$,…(11分)
| θ | $({\frac{π}{4},\frac{π}{3}})$ | $θ=\frac{π}{3}$ | $({\frac{π}{3},\frac{π}{2}})$ |
| h′(θ) | - | 0 | + |
| h(θ) | ↘ | 极小值 | ↗ |
点评 本题主要考查数学建模和解决实际问题的能力,考查运算求解能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-2,1) | C. | (2,1) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
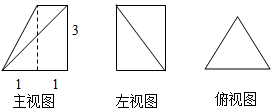
| A. | 4 | B. | 6 | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com