
分析 (1)若函数f(x)的单调递增区间是(-1,+∞),故函数f(x)的图象是开口朝上,且以直线x=-1为对称轴的抛物线,解得a值;
(2)若函数f(x)在区间(0,1)上不是单调函数,则0<$\frac{a-1}{a}$<1,解得实数a的取值范围;
(3)当a=0时,f(x)=2x-3在R上为增函数,满足条件;
当a<0时,若函数f(x)的定义域为[0,2],且f(x)在x=2时取得最大值,则$\frac{a-1}{a}$≥2,
当a>0时,若函数f(x)的定义域为[0,2],且f(x)在x=2时取得最大值,则$\frac{a-1}{a}$≤1,
综合满足条件的a的范围,可得答案.
解答 解:(1)∵函数f(x)=ax2-2(a-1)x-3,
若函数f(x)的单调递增区间是(-1,+∞),
故函数f(x)的图象是开口朝上,且以直线x=-1为对称轴的抛物线,
故$\left\{\begin{array}{l}a>0\\-1=\frac{a-1}{a}\end{array}\right.$,
解得:a=$\frac{1}{2}$;
(2)若函数f(x)在区间(0,1)上不是单调函数,
则0<$\frac{a-1}{a}$<1,
解得:a>1;
(3)当a=0时,f(x)=2x-3在R上为增函数,满足条件;
当a<0时,若函数f(x)的定义域为[0,2],且f(x)在x=2时取得最大值,则$\frac{a-1}{a}$≥2,解得:-1≤a<0,
当a>0时,若函数f(x)的定义域为[0,2],且f(x)在x=2时取得最大值,则$\frac{a-1}{a}$≤1,解得:a>0,
综上所述,a≥-1
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>y,则x>|y|”的逆命题 | B. | 命题“x>1,则x2>1”的否命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2>x,则x>1”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
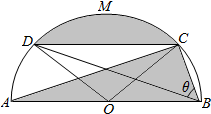 如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.
如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}\;km$ | B. | $\sqrt{13}\;km$ | C. | $\sqrt{19}\;km$ | D. | $\sqrt{10-3\sqrt{3}}\;km$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com