
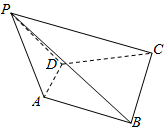
 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90°,且PA⊥AB,PD⊥CD.
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90°,且PA⊥AB,PD⊥CD.分析 (1)运用线面垂直的判定定理,结合平行线的性质,即可得到结论;
(2)由线面垂直的性质和判定,可得PA⊥平面ABCD,再由面面垂直的判定定理,即可得证.
解答 解:(1)CD和平面PAD垂直.
理由:由∠BCD=90°,AD∥BC,可得CD⊥AD,
又CD⊥PD,且AD∩PD=D,可得CD⊥平面PAD;
(2)证明:由(1)可得CD⊥平面PAD,
即有CD⊥PA,又PA⊥AB,
且AB,CD为相交二直线,
即有PA⊥平面ABCD,
又PA?平面PAD,可得面PAD⊥面ABCD.
点评 本题考查线面垂直和慢慢成长的判定,注意运用线面垂直和面面垂直的判定定理,考查转化思想和推理能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
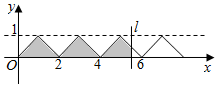 如图所示,若干个斜边长为2的等腰直角三角形的斜边在x轴上,横坐标为x的直线l自y轴开始向右匀速移动,设所有的三角形被直线l掠过的阴影部分的面积为f(x),则在定义域[0,+∞)内,关于函数f(x)的判断正确的是( )
如图所示,若干个斜边长为2的等腰直角三角形的斜边在x轴上,横坐标为x的直线l自y轴开始向右匀速移动,设所有的三角形被直线l掠过的阴影部分的面积为f(x),则在定义域[0,+∞)内,关于函数f(x)的判断正确的是( )| A. | f(x)是周期函数 | B. | f(x)-2=f(x+1) | C. | f(x+2)-1=f(x) | D. | f(x)-1=f(x+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1] | B. | [-2,-1] | C. | (-∞,-1]∪[0,+∞) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com