练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数在区间上的单调递减区间是                           （    ）

        A．                         B．

        C． D．

     

    【答案】

    D

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011-2012学年安徽省皖南八校高三第一次联考文科数学试卷解析版 题型：解答题

    （本小题满分13分）已知函数

    （I）求函数的单调区间；

    （II）若，在（1，2）上为单调递

     

    减函数。求实数a的范围。

     

    查看答案和解析>>

    科目：高中数学 来源：2010年福建省高一上学期期中考试数学卷 题型：解答题

    （本小题满分9分）以下是用二分法求方程的一个近似解（精确度为0.1）的不完整的过程，请补充完整。

    区间

    中点

    符号

    区间长度

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    解：设函数，其图象在上是连续不断的，且在上是单调递______（增或减）。先求_______，______，____________。

    所以在区间____________内存在零点，再填上表：

    下结论：_______________________________。

    （可参考条件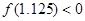：，；符号填＋、－）

     

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试理科数学（北京卷解析版） 题型：解答题

    已知函数，（），

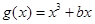
    （1）若曲线与曲线在它们的交点（1，c）处具有公共切线，求a,b的值

    （2）当时，若函数的单调区间，并求其在区间（-∞，-1）上的最大值。

    【解析】（1）， 

    ∵曲线与曲线在它们的交点（1，c）处具有公共切线

    ∴，

    ∴

    （2）令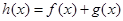，当时，

    令，得

    时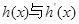，的情况如下：

    x

    +

    0

    -

    0

    +

     

     

    所以函数的单调递增区间为，，单调递减区间为

    当，即时，函数在区间上单调递增，在区间上的最大值为，

    当且，即时，函数在区间内单调递增，在区间上单调递减，在区间上的最大值为

    当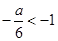，即a>6时，函数在区间内单调递赠，在区间内单调递减，在区间上单调递增。又因为

    所以在区间上的最大值为。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分15分）

    已知函数。

    ⑴求函数的最小值，并求取得最小值时的值；

    ⑵将得图象向右平移个单位后得到函数的图象，使得在区间上单调递

    增，写出一个满足条件的函数的解析式。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分9分）

     　以下是用二分法求方程的一个近似解（精确度为0.1）的不完整的过程，请补充完整。

    区间

    中点

    符号

    区间长度

    解：设函数，

    其图象在上是连续不

    断的，且在上是

    单调递______（增或减）。

    先求_______，

    ______，

    ____________。

    所以在区间____________内存在零点，再填上表：

    下结论：_______________________________。

    （可参考条件：，；符号填＋、－）

    查看答案和解析>>

    同步练习册答案