
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() .
.
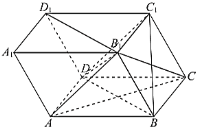
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 是等边三角形,求点
是等边三角形,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,可知点
,可知点![]() 为
为![]() 的中点,利用等腰三角形三线合一的性质可得出
的中点,利用等腰三角形三线合一的性质可得出![]() ,利用菱形的性质可得出
,利用菱形的性质可得出![]() ,可得出
,可得出![]() 平面
平面![]() ,结合面面垂直的判定定理可得出结论;
,结合面面垂直的判定定理可得出结论;
(2)计算出![]() ,并推导出
,并推导出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而可得出
,进而可得出![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,即为
的距离相等,即为![]() .
.
(1)如图,设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
因为四边形![]() 为菱形,故
为菱形,故![]() ,
,![]() 为
为![]() 的中点.
的中点.
又![]() ,故
,故![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,故
,故![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)底面![]() 是边长为
是边长为![]() 的菱形,又
的菱形,又![]() ,所以
,所以![]() ,
,![]() .
.
又![]() 是等边三角形,可得
是等边三角形,可得![]() ,
,![]() ,
,![]() .
.
由(1)可知![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,则
,则![]() ,所以
,所以![]() .
.
设![]() 交
交![]() 于点
于点![]() ,
,

又![]() ,
,![]() ,所以平行四边形
,所以平行四边形![]() 为菱形,故
为菱形,故![]() .
.
又![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() 为
为![]() 在平面
在平面![]() 内的射影,故点
内的射影,故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故点![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,
的距离相等,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.



科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() ,
,![]() 是直线
是直线![]() 上一动点.
上一动点.
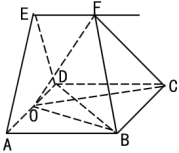
(1)求证:![]() ;
;
(2)若直线![]() 上存在唯一一点
上存在唯一一点![]() 使得直线
使得直线![]() 与平面
与平面![]() 垂直,求此时二面角
垂直,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体质健康测试中,某辅导员随机抽取了12名学生的体质健康测试成绩做分析,得到这12名学生的测试成绩分别为87,87,98,86,78,86,88,52,86,90,65,72.

(1)请绘制这12名学生体质健康测试成绩的茎叶图,并指出该组数据的中位数;
(2)从抽取的12人中随机选取3人,记![]() 表示成绩不低于76分的学生人数,求
表示成绩不低于76分的学生人数,求![]() 的分布列及期望
的分布列及期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 是轨迹
是轨迹![]() 上横坐标为2的点,
上横坐标为2的点,![]() 的平行线
的平行线![]() 交轨迹
交轨迹![]() 于
于![]() ,
,![]() 两点,交轨迹
两点,交轨迹![]() 在
在![]() 处的切线于点
处的切线于点![]() ,问:是否存在实常数
,问:是否存在实常数![]() 使
使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现中华民族伟大复兴之梦,把我国建设成为富强民主文明和谐美丽的社会主义现代化强国,党和国家为劳动者开拓了宽广的创造性劳动的舞台.借此“东风”,某大型现代化农场在种植某种大棚有机无公害的蔬菜时,为创造更大价值,提高亩产量,积极开展技术创新活动.该农场采用了延长光照时间和降低夜间温度两种不同方案.为比较两种方案下产量的区别,该农场选取了40间大棚(每间一亩),分成两组,每组20间进行试点.第一组采用延长光照时间的方案,第二组采用降低夜间温度的方案.同时种植该蔬菜一季,得到各间大棚产量数据信息如下图:
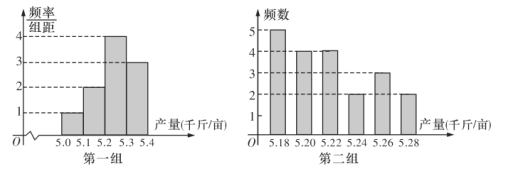
(1)如果你是该农场的负责人,在只考虑亩产量的情况下,请根据图中的数据信息,对于下一季大棚蔬菜的种植,说出你的决策方案并说明理由;
(2)已知种植该蔬菜每年固定的成本为6千元/亩.若采用延长光照时间的方案,光照设备每年的成本为0.22千元/亩;若采用夜间降温的方案,降温设备的每年成本为0.2千元/亩.已知该农场共有大棚100间(每间1亩),农场种植的该蔬菜每年产出两次,且该蔬菜市场的收购均价为1千元/千斤.根据题中所给数据,用样本估计总体,请计算在两种不同的方案下,种植该蔬菜一年的平均利润;
(3)农场根据以往该蔬菜的种植经验,认为一间大棚亩产量超过5.25千斤为增产明显.在进行夜间降温试点的20间大棚中随机抽取3间,记增产明显的大棚间数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日我国隆重纪念了建国70周年,期间进行了一系列大型庆祝活动,极大地激发了全国人民的爱国热情.某校高三学生也投入到了这场爱国活动中,他(她)们利用周日休息时间到社区做义务宣讲员,学校为了调查高三男生和女生周日的活动时间情况,随机抽取了高三男生和女生各40人,对他(她)们的周日活动时间进行了统计,分别得到了高三男生的活动时间(单位:小时)的频数分布表和女生的活动时间(单位:小时)的频率分布直方图.(活动时间均在![]() 内)
内)
活动时间 |
|
|
|
|
|
|
频数 | 8 | 10 | 7 | 9 | 4 | 2 |
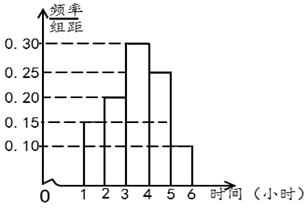
(1)根据调查,试判断该校高三年级学生周日活动时间较长的是男生还是女生?并说明理由;
(2)在被抽取的80名高三学生中,从周日活动时间在![]() 内的学生中抽取2人,求恰巧抽到1男1女的概率.
内的学生中抽取2人,求恰巧抽到1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com